Answer the question
In order to leave comments, you need to log in
How to find the maximum area?
Need to find the maximum area of a triangle with a = const and alpha = const
I had an idea to explore the function S(a, alpha) and find its max value.
But I do not understand how to represent the dependence of the area only on the angle and the opposite side ...
PS Yes, the area is through the half-product of the sides by the sine alpha and the connection of the sides through the cosine theorem, but even it does not work.
PPS we go through functions of several variables, finding extrema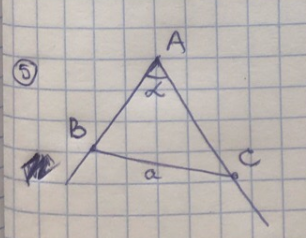
Answer the question
In order to leave comments, you need to log in
Thanks everyone. But it didn't have to be that way :D Using the diff calculus, it is solved by the method of Lagrange multipliers

I suspect that the maximum area will be obtained if AB=AC. This can even be proved by taking an isosceles triangle with side a and drawing the other side equal to a side by side. It can be shown that the triangle "above" is always larger than the triangle "below". Those. more is taken away from the area than added.
As for the function, you need to take the formula for calculating the area by the side and two angles (the second angle will be the optimizing argument).
S = 1/2*a^2*sin (180 - α - β)* sin β/sin α
The easiest way is to vary one of the remaining angles, for example B -- from 0 to pi - alpha and calculate the area as a function of it:
S = 1 / 2 * a^2 * sin(B) * sin(pi - alpha - B) / sin(alpha)Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question