Answer the question
In order to leave comments, you need to log in
How to find the coordinates of the vertices of a triangle inscribed in another triangle?
Hello, I have a question about an isosceles triangle.
We know the coordinates of the vertex of the triangle, the triangle itself is isosceles.
It is also known l is the distance (perpendicular) from the black line to the red one.
The angle shown in the figure is also known, it is equal to the angle of the small triangle.
How to calculate the coordinates of the vertices of a triangle (red) if the above values are known.
Figure - where you need to find the coordinates (a', b', c')
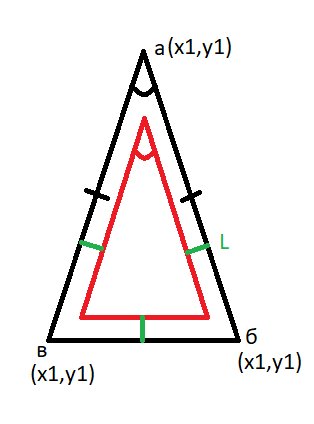
Thank you in advance for your answer.
ps Sorry for the picture.
Answer the question
In order to leave comments, you need to log in
I will not write a complete solution so that your brains have work to do. But here's a big hint.
x(a')=x(a) (assuming according to the drawing that y(b)=y(c));
y(a')=y(a)-(lilac hypotenuse length);
the upper corner of a right triangle is known as half the vertex angle a; the green leg is known as L, we can calculate the hypotenuse. Then we calculate the angle at the vertex b and repeat the same reasoning. Only there you need to calculate not the hypotenuse, but the second leg. And you're done.
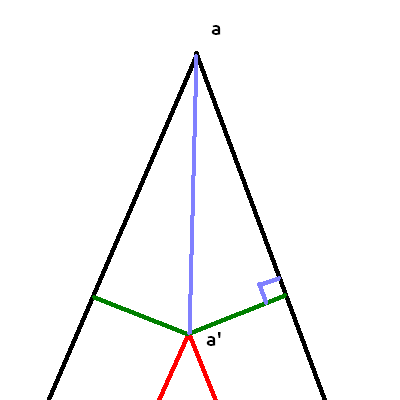
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question