How to find a point at a distance d from a straight line?

Question

Mathematics

Hello, I need to solve a problem. Namely, there is a polyline (given by an array of points) and you need to find a polyline that envelops the original one, it will probably be more clear in the figure (blue is the one you need to build):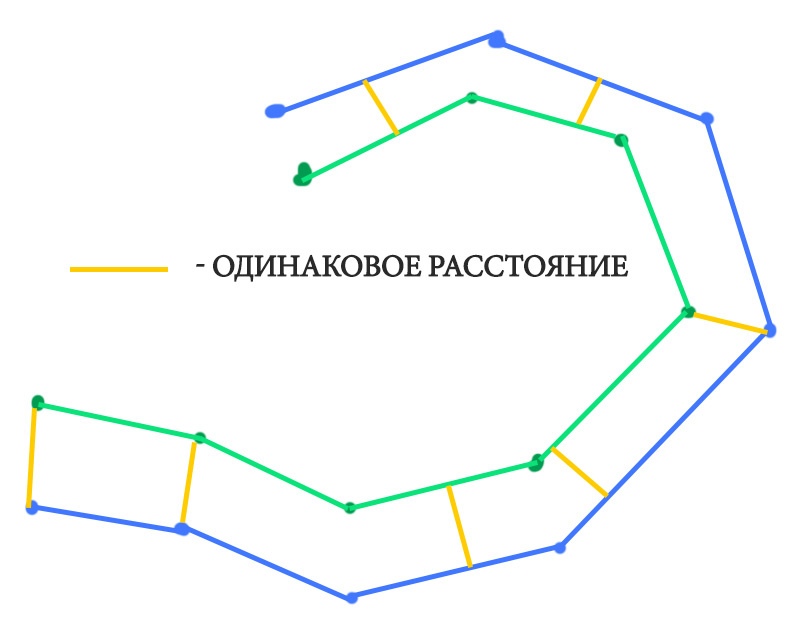
That is, if you build a polyline using new points, it should repeat and go around initial. What formulas can be used to calculate this if a two-dimensional array with points is given?

Answer 1

Find a center. Draw perpendiculars. Scalar coordinate system.

Answer 2

You have an error in your assignment. The envelope is not a broken line (a set of segments), but a more complex line.
When the envelope goes along a straight section, it will also be straight. But when rounding the top - there will be a circle.
Let's look at the first segment. Let it be given by the start points {x0,y0} and end points {x1,y1}.
Let's calculate the vector of this segment v={(x1-x0),(y1-y0)}.
Let's calculate the normal to it n={(y1-y0),(x0-x1)} - change the coordinates in places, change the sign of one of the coordinates.
We normalize the normal, i.e. we calculate the length of the normal (Pythagoras suggests) and then divide each component by the length. Those. the normal is of unit length.
Multiply the normal (each component) by the length of the yellow segment.
Now let's add this normal to the first point {x0,y0} and then to the second point {x1,y1}. We get the ends of the first blue segment.
One trouble - the blue segments obtained in this way will be equal to the original ones, and therefore do not fit.
In order to join them - you need to look for the intersection of lines. In theory, there is nothing complicated.