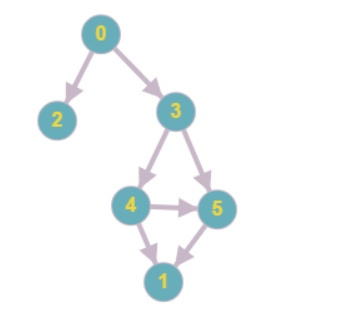
How to find a path in a directed graph?

Question

Java

Where is the mistake? The algorithm only visits nearest neighbors.

public boolean path(int from, int to) {
        //массив посещений графов
        boolean[] visited = new boolean[getAllNodes().size()];
        dfs(from, visited);

        return visited[to];
    }

    public void dfs(int index, boolean[] visited) {
        Stack<Integer> stack = new Stack<>();

        stack.push(index);
        visited[index] = true;

        while(!stack.isEmpty()) {
            Integer nodeIndex = stack.pop();
            visited[nodeIndex] = true;
            //Заполняем список потомков
            List<Integer> neighboursList = new ArrayList<>(getChildrenOf(index));

            for(Integer neighbour: neighboursList) {
                if(!visited[neighbour]) {
                    stack.push(neighbour);
                }
            }
        }
        for (int i = 0; i < visited.length; i++) {
        }
    }

Graph
And is it possible with the help of this algorithm to remember the path, and not just its presence true/false

Answer 1

0) you have a loop in your code that does nothing, you can remove it.
1) in the line where the list of neighbors is obtained, the wrong variable is used. The current vertex is stored in nodeIndex.
2) you can remember. To do this, either an additional array is used, in which the "ancestor" of the vertex v is stored, that is, such a vertex u, after considering which, v was added to the stack. As a result, to get the path, it will be necessary to unwind the chain of ancestors from the final vertex to the starting
2.5) if you need the shortest path in an unweighted graph (all edges are the same), then you should use the BFS algorithm (use a queue instead of a stack). If the graph is weighted, then Dijkstra's algorithm is used

Answer 2

1. The answer to your question is "You can".
2. Anticipating your next question - "how can this be done" - I will answer right away, I don’t know what path you decided to look for there (you didn’t even bother to tell us about it - but why, you still have to run to guess what task is there you were given a homework assignment and you did not master it - but oh well) - but start searching for paths in a directed graph with Daysktra's algorithm. 99% of the questions will disappear (if you master, of course). For other misunderstandings - come back here, we'll try to help.