Answer the question
In order to leave comments, you need to log in
How to explain the problem in combinatorics?
Please explain the solution to this problem
Task:
You need to learn 11 topics for the exam. The six students agreed that each would learn two topics and share the material with the others. In how many ways can the topics be distributed among the students so that each topic remains learned (one of the topics will be learned by two different students)
Solution:
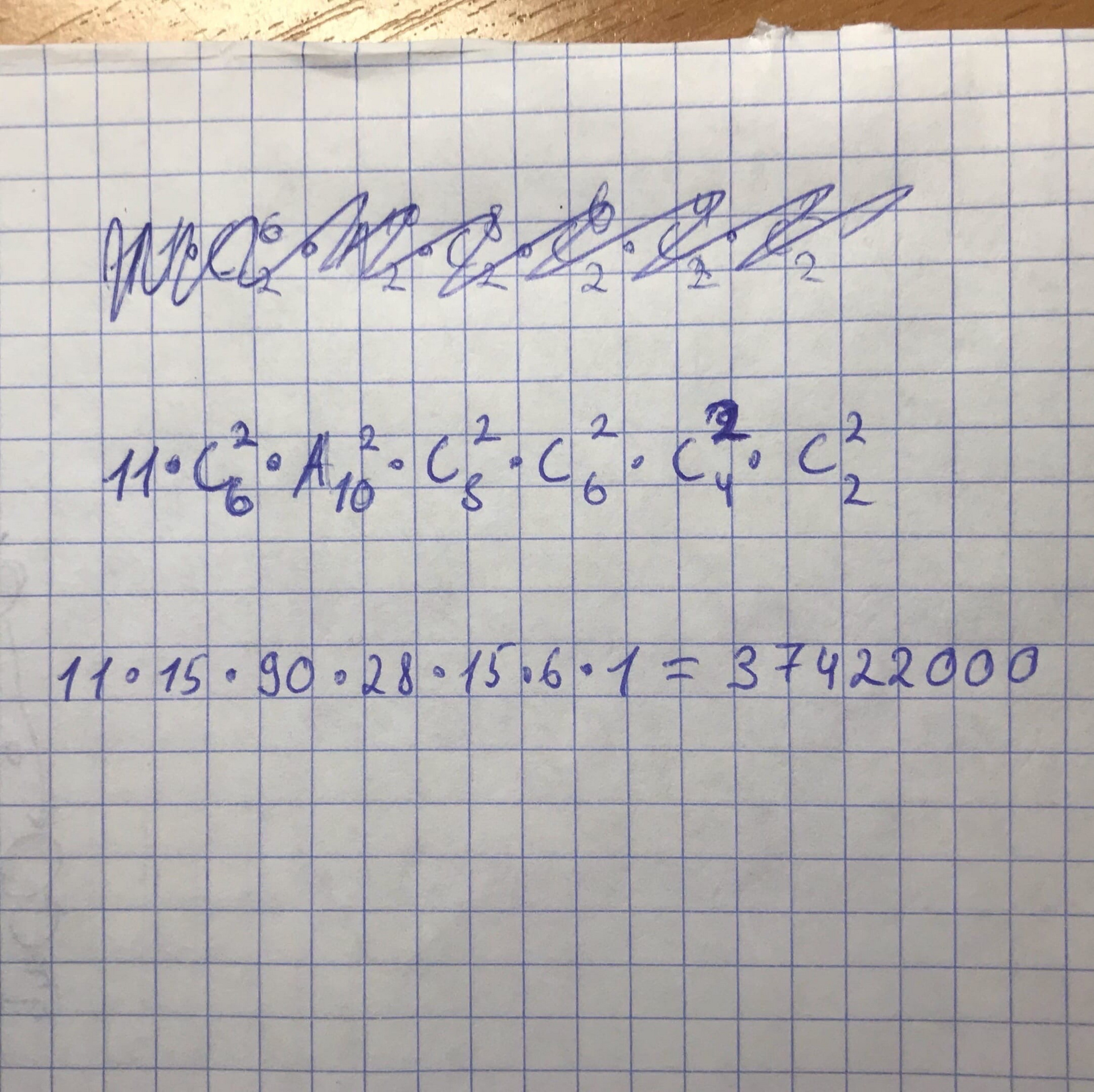
Answer the question
In order to leave comments, you need to log in
Try this.
window.onscroll = function() {
var scrolled = window.pageYOffset || document.documentElement.scrollTop;
document.getElementById('name').className += 'red';
}You first choose the topic that 2 students will learn. She is clearly different from everyone else. These are 11 options. This is the first multiplier of 11 in the answer.
Then, all options differ in which 2 students will learn this topic. This is the C(2.6) multiplier.
Next, these 2 students must learn one more topic. This is to choose 2 topics from the remaining 10. But here the order is important, because these are different topics for different students. This is the A(10,2) multiplier.
What's left? 8 unlearned topics and 4 students. There is a well-known formula for generalized combinations or combinations of several colors (I don’t remember the exact name). There will be 8 such combinations!/(2!*2!*2!*2!). The same formula can be obtained by sequentially choosing 2 topics for each of the four students. The first one can take the topics C(2,8) variants. The second of the remaining 6 topics is C(2,6) variants and similarly for the third and fourth students (C(2,4) and C(2,2)).
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question