How to efficiently find max. the value of an ever-increasing quantity?

Question

Algorithms

The integer value is constantly growing as a result of the activity of social network users. Is there an API through which you can only find out if the value X already exists or not? I would like to know at any time what value is currently the largest of the created ones, by making a minimum of requests to the API (suppose the requests are paid).
Some history of values ​​has already accumulated and you can try to build a model - a linear or hyperbola. But the longer there were no new measurements, the greater the possible spread from the predicted one.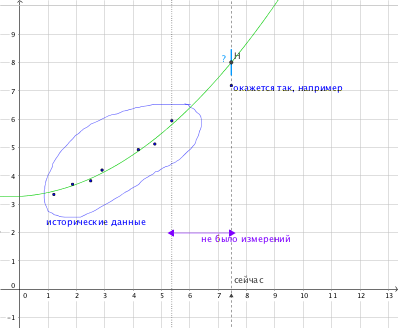

A very rough version without a model is a binary search in the range from the last found value (lower bound) to some large value (empirical) up.
Question: how to properly search using the scientific methodpoke, if you build the same model that fits into the historical data in order to minimize the number of poke?
Those. from the model, a hypothesis is obtained that at a given point in time the value will reach the value H. You can check it: it either exists or it does not exist yet. What step now to step back from H to make the next check?

Answer 1

Some kind of vague question you have turned out, from which what I said is possible for you to understand.
If there is a certain spline based on the old results, then why not start from it and get a certain number N.
Next, check whether N+M and NM have been reached.
Accordingly, finding out whether the desired value is in the segment [N+M; NM].
M - pre-calculate from the spread of values ​​from the spline and your required accuracy.
If M turns out to be too large and the accuracy does not suit you, then you will have to do this several times.
If M turns out to be less than the spread, then more checks (i.e. queries) will have to be done.
If it was possible to predict only a certain spline, without any patterns, then this is the only option.
With this approach, calculating the exact number is still expensive ...
PS You should not check the number N itself (you called it H), since the spread will still be. You need to take a fairly wide segment, check its edges, and then cut it in half (Ie, the logarithmic search algorithm).

Answer 2

Google: Approximation.
Extrapolation.