How to determine the slope of a square with a known side from its Bounding Box?

Question

Images

Hello,
there are squares in the image with a known side length, I need to know the slope about the x-axis. The MATLAB regionprops function returns the axis-aligned Bounding Boxes. As I reasoned:
Let the width of the boundingbox w, the side of the square c, the angle of inclination alpha. Then

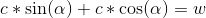
Use the Weerstrass substitution Simplify

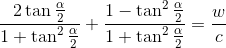
the equation Solve the

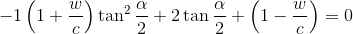
quadratic equation with respect to tan(alpha/2) , coefficients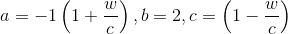

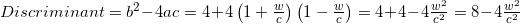
For a non-zero slope, the discriminant is positive

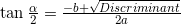
The logic seems to be correct, the calculations too, but the answer is wrong. Tell me, please, what I made a mistake, and advise a way to accurately determine the slope of the actual square inscribed in the square.
Here is an example in MATLAB

img = false(25,25);
img(5:16,5:16) = true;
rot_img = imrotate(img, 30, 'crop');
props = regionprops(bwlabel(rot_img),'BoundingBox');
bbox = cat(1,props.BoundingBox);
w = bbox(3);
h = 12;
a = -1*(1+w/h); b = 2; c = 1 - w/h;
D = b^2 - 4*a*c;
alpha = 2*atand((-b + sqrt(D))/(2*a));
%alpha = 25.5288

EDIT Thanks for the clarification on trigonometry, I've had a difficult relationship with her since high school.
I realized that I asked the question incorrectly, more precisely it should sound like this: how exactly (+/- 0.5 degrees) to determine the slope of short lines (10-50 pixels)? The position of the lines is not important, only the slope.
I played with the formulas from the answers, it is clear that they give the same, but far from the desired answer, while the calculation result improves with the growth of the linear size of the object. So, we run into rasterization, and we need to look for a relatively "light" algorithm in terms of speed with subpixel resolution. So far I have found only the search for lines through the Radon transform:

p = bwperim(rot_img);
theta=0:0.1:179.9;
[R,xp] = radon(p,theta); %Преобразование Радона
a=imregionalmax(R,true(3,3)); %Локальные двумерные максимумы преобразования Радона
[r,c]=find(a); idx=sub2ind(size(a),r,c); maxvals=R(idx);
[val,midx]=sort(maxvals,'descend');
mean(rem(theta(c(midx(1:4))),90)) %Выбираем 4 самых больших локальных максимума
%29.85

EDIT2 sample image after binarization After scanning, you need to align the image. Greater accuracy and speed are needed, and the quality of scanning can be anything, including very low.

Answer 1

w/c=sin(a)+cos(a)
(w/c)^2=1+sin(2a)
sin(2a)=(w/c)^2-1
a=0.5*arcsin((w/c)^2-1)

Answer 2

Why is it so difficult?! There is a formula.
here formula (24)
or here it is also number 9
w/c = sin(alpha)+cos(alpha) = sqrt(2)*sin(alpha+Pi/4)
PS

We use the Weerstrass substitution

It is customary to write his last name like this: Weierstrass.