How to determine from the truth table and the circuit which logical functions are present?

Question

Electronics

How conditionally looking at the truth table and according to the scheme with a multiplexer, for example, determine its structure.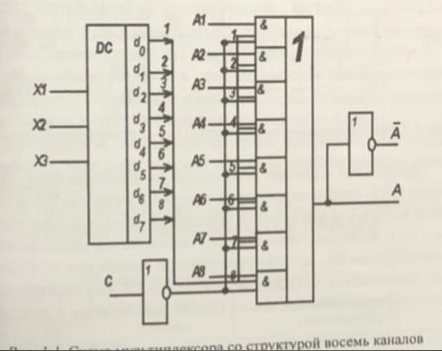
Here, in this picture you can see that there is a logical function "Or" and an Inverted "And", and how you can understand this yourself. The teacher showed us somehow conditionally, closing the column on the truth table and asked what element it looked like. And how to write an equation based on the truth table?
 

Answer 1

The truth table expresses one logical function that can be described in different ways (perfect disjunctive normal form or perfect conjunctive normal form, for example, or their funny variants).
A multiplexer can describe any truth table for n inputs, if n is the number of address inputs of the multiplexer (I can tell you in more detail how, if you're interested).
According to the truth table itself, the structure cannot be restored if the table does not describe any simple logical element (and, or, not, and-not, etc.).
It is impossible to restore the structure for the reason that the same logical function can be described in different ways (as I said above SDNF, SKNF, etc.).
From the truth table, you can restore its function by different methods, one of the most common and visual methods is Karnaugh maps. At first glance, it looks like black magic, but you need to strain your brain a little - and everything falls into place. If needed, I can explain how to use it.

Answer 2

And how to write an equation based on the truth table?

Well, just write the equation until all the conditions pass.
You can stupidly turn each row of the table into a subexpression.
Here's an example I just came up with:

A B C R
1 1 1 0
1 1 0 0
1 0 1 1
1 0 0 1
0 1 1 1
0 1 0 0
0 0 1 1
0 0 0 1

It all eventually turns into something like this equation (we take all the combinations that result in the truth)

R = (A & !B & C) | (A & !B & !C) | (!A & B & C) | (!A & !B & C) | (!A & !B & !C)

It remains to simplify:
R = A & !B | !A & ((B & C) | !B )