How to derive a formula for equivalence?

Question

Mathematics

//Можно опустить: Решил развить логику, начал изучать лекции "введение в логику". 
Честно, дается очень трудно, но спустя 2-3 часов штурма доказательства обычной 
теоремы/формулы (наверно любой другой бы за 5 мин понял) наступает эйфория. 
все сложнее и сложнее, хотя только начало...

there is a formula:

It must be proved using the Zhigalkin bases.
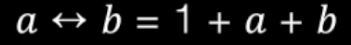
Aizhu only (1+a)replaced with ¬acomes out ¬a+b.

Answer 1

As I understand it, in the task it is required to bring to the Zhegalkin polynomial. The right side already matches.
Equivalence in disjunctive form: A<=>B = AB v (-A)(-B) (this is practically by definition)
Use the disjunction formula: A v B = A + B + AB (of course, it also needs to be justified, but I am sure that such an expression should be proved earlier).
Then, using some properties of Boolean algebra and, in particular, the sum operation:
AB v (-A)(-B) = AB + (-A)(-B) + AB(-A)(-B) = AB + ( -A)(-B) = AB + (A+1)(B+1) = AB + AB + A + B + 1 = A + B + 1
Of course, this method is not the only one. Still, for example, it is possible to make truth tables for both expressions. Or notice that the equivalence is the inverted sum, that is, the sum + 1. Or reduce both parts to DNF/CNF.