Answer the question
In order to leave comments, you need to log in
How to create a cylindrical helix?
Need to create a helix in 3d space.
I have the code to create a helix:
float t = distance/100.0; // Š“Š»ŠøŠ½Š° Š»ŠøŠ½ŠøŠø
pos2[0] = StartPos[0]; // Š½Š°ŃŠ°Š»ŃŠ½Š°Ń ŠæŠ¾Š·ŠøŃŠøŃ StartPos(ŃŠ¾ŃŠŗŠ° Š²Š¾ŠŗŃŃŠ³ ŠŗŠ¾ŃŠ¾ŃŠ¾Š¹ Š±ŃŠ“ŠµŃ ŃŠøŃŠ¾Š²Š°ŃŃŃŃ Š¾ŠŗŃŃŠ¶Š½Š¾ŃŃŃ)
pos2[1] = StartPos[1] + radius;
pos2[2] = StartPos[2];
while (angle <= PI*t){
x = radius * Cosine(angle);
y = radius * Sine(angle);
pos1[0] = pos2[0] + t;
pos1[1] = pos2[1] + x;
pos1[2] = pos2[2] + y;
ŠŠ“ŠµŃŃ ŃŃŠ½ŠŗŃŠøŃ ŃŠøŃŠ¾Š²Š°Š½ŠøŃ Š»ŠøŠ½ŠøŠø.........................
pos2 = pos1;
angle += PI/10.0; // ŠŗŠ¾Š»ŠøŃŠµŃŃŠ²Š¾ ŃŠµŠ³Š¼ŠµŠ½ŃŠ¾Š² Š¾ŠŗŃŃŠ¶Š½Š¾ŃŃŠø (PI/10 - 10 ŃŠµŠ³Š¼ŠµŠ½ŃŠ¾Š²)
}Answer the question
In order to leave comments, you need to log in
You can multiply the resulting coordinates by the desired transformation matrix.
https://habr.com/ru/post/319144/ section "Rotation matrix"
The matrix is āācalculated once before drawing, and then all the coordinates of the spiral are multiplied by it.
Example:
We have a vector around which we want to rotate the entire spiral: (vx,vy,vz)
There is an angle we want to rotate: a
Then the rotation matrix around this vector looks like this:
{
{cos(a)+(1-cos(a))*vx*vx, (1-cos(a))*vx*vy-sin(a)*vz, (1-cos(a))*vx*vz+sin(a)*vy, 0},
{(1-cos(a))*vy*vx+sin(a)*vz, cos(a)+(1-cos(a))*vy*vy, (1-cos(a))*vy*vz-sin(a)*vx, 0},
{(1-cos(a))*vz*vx-sin(a)*vy, (a-cos(a))*vz*vy+sin(a)*vx, cos(a)+(1-cos(a))*vz*vz, 0},
{0, 0, 0, 1}
}a=cos(a)+(1-cos(a))*vx*vx
b=(1-cos(a))*vx*vy-sin(a)*vz
c=(1-cos(a))*vx*vz+sin(a)*vy
d=(1-cos(a))*vy*vx+sin(a)*vz
e=cos(a)+(1-cos(a))*vy*vy
f=(1-cos(a))*vy*vz-sin(a)*vx
g=(1-cos(a))*vz*vx-sin(a)*vy
h=(a-cos(a))*vz*vy+sin(a)*vx
i=cos(a)+(1-cos(a))*vz*vz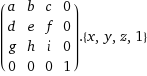
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question