How to change the Kalman filter so that the result is similar to the envelope of the original signal in Matlab?

Question

Signal processing

I took the implementation of the Kalman filter from these articles: https://clck.ru/FSbT2, https://habr.com/ru/post/166693/
In my task, a signal is given in the condition, which looks like this: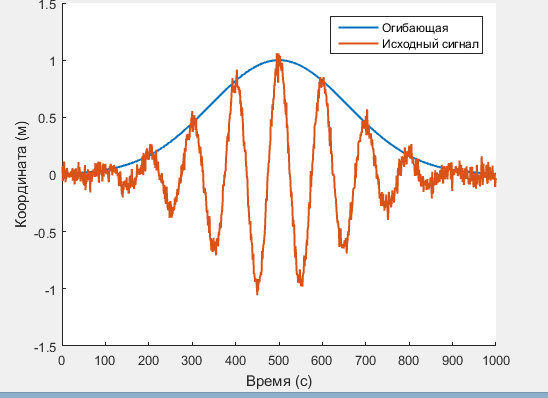

for x = 1:N
    A(x) = exp((-(x-500)^2)/50000);
    y(x) = A(x)*cos(2*3.14*0.01*x)+normrnd(0,sigmaPsi);
end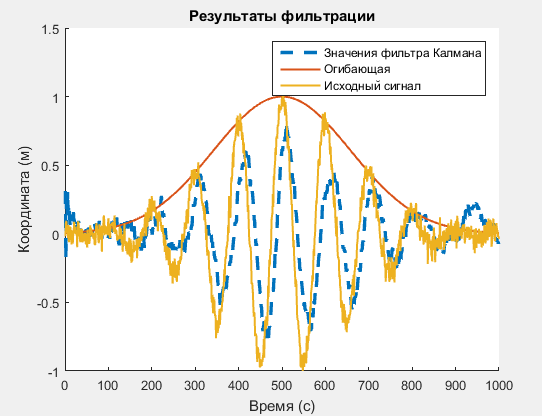

After applying the Kalman filter, we got a result that practically repeats the original signal (as in the problem from the above sources):

I need the Kalman filter graph to be closest not to the original signal, but to its envelope. Accordingly, you need to slightly change the Kalman filter algorithm itself:

for t=1:(N-1)
    eOpt(t+1)=sqrt((sigmaEtaFilter^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEtaFilter^2+eOpt(t)^2+sigmaPsi^2)); %минимизация значения ошибки
    msum = msum + eOpt(t+1);
    sum = sum + (eOpt(1))^2;
    K(t+1)=(eOpt(t+1))^2/sigmaEtaFilter^2; %выражение для ошибки
    xOpt(t+1)=(xOpt(t))*(1-K(t+1))+K(t+1)*z(t+1);
end;

How can I do that ? I have been trying to figure it out for a long time, but so far to no avail.
Program code :

N = 1000;
sigmaPsi=0.05; %реальные погрешности (ошибка модели)
sigmaEtaModel=0.5; %ошибка измерений прибора
sigmaEtaFilter = 0.8;
k=1:N;
x=k;
for x = 1:N
    A(x) = exp((-(x-500)^2)/50000);
    y(x) = A(x)*cos(2*3.14*0.01*x)+normrnd(0,sigmaPsi);
    z(x)=y(x)+normrnd(0,sigmaEtaModel); 
end
%kalman filter 
xOpt(1)=z(1); %хорошее приближение для истинной координаты
eOpt(1)=sigmaEtaFilter; %дисперсия
msum = eOpt(1); 
sum = (eOpt(1))^2; 
for t=1:(N-1)
    eOpt(t+1)=sqrt((sigmaEtaFilter^2)*(eOpt(t)^2+sigmaPsi^2)/(sigmaEtaFilter^2+eOpt(t)^2+sigmaPsi^2)); %минимизация значения ошибки
    msum = msum + eOpt(t+1);
    sum = sum + (eOpt(1))^2;
    K(t+1)=(eOpt(t+1))^2/sigmaEtaFilter^2; %выражение для ошибки
    xOpt(t+1)=(xOpt(t))*(1-K(t+1))+K(t+1)*z(t+1);
end;
sr = msum/N;
vdisp = sum/N - sr^2; 


hold all;
plot(k,xOpt,'--','linewidth',2.5);
plot(k,A,'linewidth',1.5);
plot(k,y,'LineWidth',1.5); 
title('Результаты фильтрации'); 
xlabel('Время (с)');
ylabel('Координата (м)'); 
legend('Значения фильтра Калмана', 'Огибающая','Исходный сигнал');

Answer 1

In my opinion, using the Kalman filter, you can only smooth the original signal, but not get the "envelope".
The signal is similar to amplitude modulation (radio signal).
https://en.wikipedia.org/wiki/Envelope_detector
https://www.mathworks.com/help/dsp/examples/envelo...