How to calculate the total resistance of a four-dimensional cube?

Question

Physics

I set out to calculate the total resistance of a four-dimensional cube between points 1 and 2 (the picture is attached), in which the resistance of one edge is R.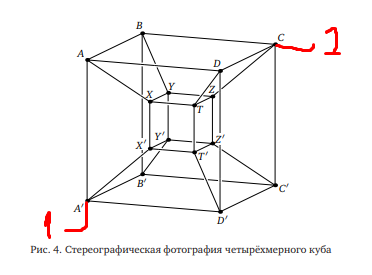

As an example, here is the calculation of the resistance of a 3-dimensional cube

Answer 1

Hey young man! The task was set, wow!
You lie, but don’t lie: if this problem came to your mind by itself, the answer would be obvious to you.
Assignment, so to speak.
Threat And if you do it yourself - it's also funny. For a three-dimensional cube, opposite vertices are taken, the shortest path between them is three edges. Between A and C in your drawing there are also 3 edges, the opposite ones are vertices A and Z.
For A and Z the solution is simple. 4 edges go out of A and Z, in total there are 32 edges in the hypercube, in total A and Z are connected by a garland of four bundles of edges: 4-12-12-4, total resistance 1/4+1/12+1/12+1 /4 == 2/3