Answer the question
In order to leave comments, you need to log in
How to calculate the sum of an infinite series using a mixed method and a general formula for calculating a term of a series. How to find a recursive formula?
It is necessary to solve the sum of an infinite series in this case, it would be nice to paint each step. I can't figure out how to properly derive formulas...
We need to find a recurrent formula and show how it was derived. It is also clear from the condition that you need to use a mixed method and a general formula.
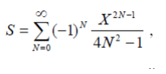
Answer the question
In order to leave comments, you need to log in
A recurrent formula is an expression of a member of a sequence through a function of its number and the values of the previous members.
z n = f(n, z n-1 , z n-2 , ...)
In your example, general recursion does not work, you need to break it into parts and find a recursive formula for each of them. Let's select the part of the formula where n is used in the exponent and the part where n is in the base of the degree.
z n = a n /b n
a n = (-1) n x 2n-1
b n = 4n 2 -1
For a nmultiplication is recurrent. Divide the term of the sequence by the previous one.
a n / a n-1 = ((-1) n x 2n-1 ) / ((-1) n-1 x 2n-3 ) = -x 2
For b n addition is recurrent. Let us subtract the previous one from the member of the sequence.
b n - b n-1 = (4n 2 - 1) - (4(n - 1) 2 - 1) = 8n - 4
We get
a 0 = 1/x, a n = -a n-1 x 2
b 0 = -1, b n = b n-1+ 8n - 4
z n = a n / b n
It remains to write this into the program.
I have no idea what kind of mixed method you need, but the sum of this series can be found twice by taking the derivative.
Let be f(x)your row. Then f'(x) = sum (-1)^n x^(2n-2) / (2n+1)
To completely get rid of the denominator it would be necessary that the degree be 2n + 1. This can be achieved by multiplying everything by x^3. Then we can take the derivative again.
(x^3 f'(x))' = sum (-1)^nx^2n = sum (-x^2)^n = 1/(1+x^
2
x^3 f'(x) = arctg(x)+C
) =0 left 0 means C=0.
f'(x) = arctg(x) / x^3
From here you can find f'(x): Go to wolframalpha and enter integrate arctg(x)/x^3 dx(I can’t give a direct link with a request for wolfram, because for some reason the mat-filter works on the link and does not allow you to send a response).
To find a constant, you have to substitute, for example, x=1 and find the sum of the series a_n = (-1)^n/(4N^2-1). This is some well-known converging rad, it seems. Again, look at wolframalpha , enter sum (-1)^n/(4*n^2-1), n=0 to infinity. As a result, it turns out that the constant there is also 0.
So it turns out thatf(x) =- (x^2 * arctan(x) + arctan(x) + x) / (2x^2)
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question