Answer the question
In order to leave comments, you need to log in
How to calculate the flight of a projectile in two-dimensional space at an angle?
Hello. It is required to calculate the trajectory of the projectile. View of the map from above, at an inclination of 45 degrees (as in many strategies). You need something like this: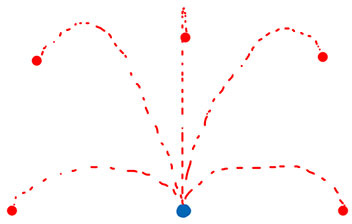
Answer the question
In order to leave comments, you need to log in
Two subtasks:
(x, y, z). (0, 0)and looks exactly at the (0, 0, 0)three-dimensional world. The screen has an axis to the Xright, an axis Yup. In the world, the axis is to the xleft, the axis is yup, the axis is zfar away. xthe same way will add X' to the screen.Ya little less screen space due to the 45° angle. Those. y multiply by the root-of-2 in half. z.X = x;
Y = (y + z) * 0.7071;Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question