How to fix the error in the calculations by the Runge-Kutta method (4 orders)?

Question

Python

Good day!

There was a problem with calculating the values ​​for plotting the Lorentz attractor.

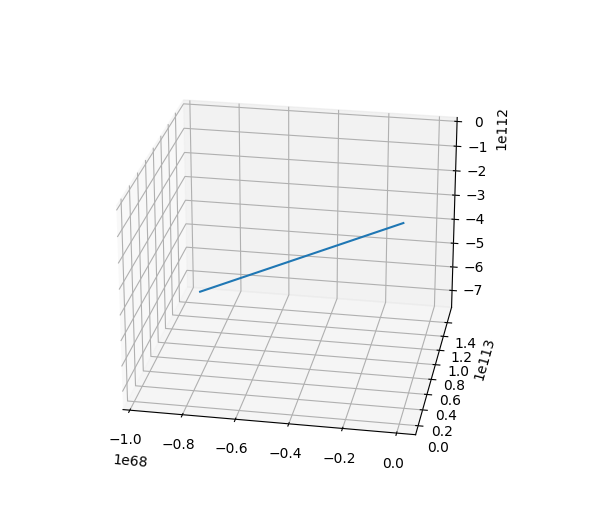
The fact is that already at 2 - 3 iterations, very large values ​​​​of the coefficients begin to appear.

The code:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

sigma = 10
r = 28
b = 8 / 3

def LorenX(x,y):
    return sigma * (x - y)
def LorenY(x,y,z):
    return x * (r - z) - y
def LorenZ(x,y,z):
    return x * y - b * z

def rg4(x0,y0,z0,dt = 0.0001):
    x = x0
    y = y0
    z = z0
    arrx = [0]
    arry = [0]
    arrz = [0]

    fig = plt.figure()
    ax = fig.add_subplot(111, projection='3d')
    for i in range(10000):

        arrx.append(x)
        arry.append(y)
        arrz.append(z)

        k1 = LorenX(x,y)
        m1 = LorenY(x,y,z)
        p1 = LorenZ(x,y,z)

        k2 = LorenX(x + k1/2,y + m1/2)
        m2 = LorenY(x + k1/2,y + m1/2,z + p1/2)
        p2 = LorenZ(x + k1/2,y + m1/2,z + p1/2)

        k3 = LorenX(x + k2/2,y + m2/2)
        m3 = LorenY(x + k2/2,y + m2/2,z + p2/2)
        p3 = LorenZ(x + k2/2,y + m2/2,z + p2/2)

        k4 = LorenX(x + k3,y + m3)
        m4 = LorenY(x + k3,y + m3,z + p3)
        p4 = LorenZ(x + k3,y + m3,z + p3)

        x += (dt * (k1 + 2*k2 + 2*k3 + k4) / 6)
        y += (dt * (m1 + 2*m2 + 2*m3 + m4) / 6)
        z += (dt * (p1 + 2*p2 + 2*p3 + p4) / 6)
    ax.plot(arrx, arry, arrz)
    plt.show()

rg4(1,1,1)

Here are the first two iterations (x,y,z values ​​respectively)

Pyplot plots such a line and three axes with inadequate values:


https://www.cyberforum.ru/cpp-beginners/thread1874... - from here I took the coefficients (last code message)

Answer 1

First:
# b = 8 / 3
# got integer division, b=2
b = 8.0/3
Second:
def LorenX(x,y):
# return sigma * (x - y)
return sigma * (y - x)
Third:

...from here I took the coefficients (last message with the code)

Wrong copypasta. You did something strange with dt. I copied and pasted from there without any gag:

#
        k1 = dt*LorenX(x,y)
        m1 = dt*LorenY(x,y,z)
        p1 = dt*LorenZ(x,y,z)

        k2 = dt*LorenX(x + k1/2,y + m1/2)
        m2 = dt*LorenY(x + k1/2,y + m1/2,z + p1/2)
        p2 = dt*LorenZ(x + k1/2,y + m1/2,z + p1/2)

        k3 = dt*LorenX(x + k1/2,y + m2/2)
        m3 = dt*LorenY(x + k1/2,y + m2/2,z + p2/2)
        p3 = dt*LorenZ(x + k1/2,y + m2/2,z + p2/2)

        k4 = dt*LorenX(x + k1,y + m3)
        m4 = dt*LorenY(x + k1,y + m3,z + p3)
        p4 = dt*LorenZ(x + k1,y + m3,z + p3)

        x += (k1 + 2*k2 + 2*k3 + k4) / 6
        y += (m1 + 2*m2 + 2*m3 + m4) / 6
        z += (p1 + 2*p2 + 2*p3 + p4) / 6