Answer the question
In order to leave comments, you need to log in
How many different unique subsequences are there from a sequence of digits of length N?
There is a sequence of numbers, for example 8 2 4 6 .
This number has 41 subsequences , they are:
8246
246, 846, 826, 824
46, 26, 24, 46, 86, 84, 26, 86, 82, 24, 84, 82
4, 6, 2, 6, 2, 4, 4, 6, 8, 6, 8, 4, 2, 6, 8, 6, 8, 2, 2, 4, 8, 4, 8, 2
With 15 unique :
8246
246, 846, 826, 824
46, 26, 24, 86, 84, 82
4, 6, 2, 8
What algorithm should be used to count the number of unique subsequences?
(Brute force doesn't work. Something more algebraic is needed.)
Answer the question
In order to leave comments, you need to log in
You can somewhat reduce the number of options when iterating by grouping consecutive identical numbers. Let's say for (1 1 1 2 1 1) we get the original set ((1, 3), (2, 1), (1, 2)). After that, iterate over it recursively.
функция рекурсия(набор, результат) {
если набор пуст {
если результат уникален {
добавить результат в список уникальных
}
}
((цифра, количество), следующий_набор) = набор;
для i от 0 до количество {
рекурсия(следующий_набор, результат+(цифра i раз));
}
}
рекурсия(исходный_набор, '');In the general case, only exhaustive search is obtained, the number of all subsequences = 2 n -1
The complete enumeration can be significantly reduced without going through specific permutations of digits: if digits d i , i = 1...m are chosen, among which there are groups of the same, with the number of digits in each of these groups c j , j = 1...k, then from these numbers you can make 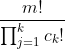
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question