Determining the position of the point with the maximum weight

Explode2012-01-02 09:42:07

Google

Explode, 2012-01-02 09:42:07

There is a coordinate plane. There are several points on it, each of which has its own weight (from 0 to 99). Their coordinates and weight are known. It is also known that in the center of all these points there is one point with a weight of 100, but its coordinates are not known. The further the other points are from it, the less their weight.
Here you need to somehow determine the position of the point with the maximum weight using several points.

Similar algorithms are implemented in programs for determining the coordinates of Wi-Fi routers by analyzing the signal in the nearby area.

Answer the question

In order to leave comments, you need to log in

8 answer(s)

vare6gin, 2012-01-02
@Explode

If the relationship between the coordinates and the point weight, for example, is linear, then you need to solve the equation: w=a*x + b*y + c. This requires 3 points.
After solving (a, b and c are found), we can express the equation of a straight line for which w=100:
y=(100 - a*x - c)/b.
Next, you need to solve w=a'*x + b'*y + c' with respect to another combination of points.
The desired point with a weight of 100 will be the intersection of y=(100 - a*x - c)/b and y=(100 - a'x - c')/b'.
Again, this is a solution for a linear relationship between coordinates and weight. If I made a mistake in reasoning (and this is very likely, since matan was a very long time ago), then write where.
Thank you.

Eddy_Em, 2012-01-02
@Eddy_Em

If there are a lot of points, it is possible to construct weight isolines and determine the position of the center from the skeletons of isoregions.

Alexey, 2012-01-02
@Squier

Determine the distance of a point from the center. By two points, you can find 2 possible options, the third one will indicate which of the two points of intersection of the circles will be the center.
Here, respectively, in coordinates. You can write circle equations for points.

VasG, 2012-01-02
@VasG

You can take points in pairs and build vectors based on them. The greater the difference in the weight of the points, the greater the "length" of the vector connecting them, the direction is determined by the point with the highest weight.
In theory, if you draw two similar vectors from one point, the angle between which will be >= Pi / 2, then there is a probability (“probability” because I’m just not sure. My inner voice tells me that this should be the case in 99% of cases ) the fact that the vertor obtained by summing the previous two will indicate the direction towards the point with the greatest weight.

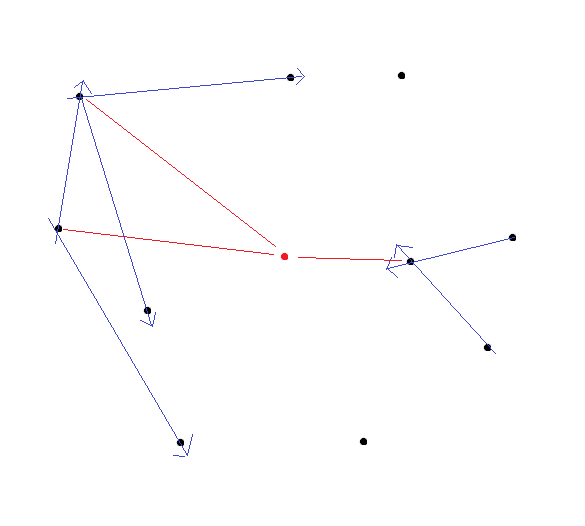
Next, you need to extend the resulting vectors to straight lines, and find the point of their intersection. The point at which the largest number of lines intersect is the desired one (I mentioned how to find the point with the largest number of intersections in my article ).

AlexanderG, 2012-01-02
@AlexanderG

You can try triangulation. To begin with, we define (arbitrarily) the correspondence between the weight and the radius of the circle (required later). Then we take three points, build for them circles of radii corresponding to their weights, we get an area bounded by the points of intersection of the circles. Next, we increase/decrease the radii of the circles, trying to reduce the area of the region bounded by the intersection points. Ultimately, this region will degenerate into a point, which will be the desired center.

Mrrl, 2012-01-03
@Mrl

Least square method. If the distance from the desired point (x,y) to one of the known (xi,yi) is equal to ri, then (x-xi)^2+(y-yi)^2-ri^2=0 (up to noise) . We build f(x,y)=Sum(((x-xi)^2+(y-yi)^2-ri^2)^2) (this is a polynomial of the 4th degree in two variables), and solve the system of equations {df/dx=0, df/dy=0} for example, Newton's method. But it's not certain that the root will be unique, so you have to try many starting points, and check the value of f for each result.

EndUser, 2012-01-05
@EndUser

I can't figure out how to solve the situation 60-90 (dots on the same line):
a)!60!-(70)-(80)-!90!-! is he!
b)!60!-(70)-(80)-(90)-! he!-!90!
!!! a real point is
indicated () a virtual one is indicated (calculated weight at a distance)
it is the desired
router

Explode, 2012-01-06
@Explode

For example, here is the result of the Ekahau HeatMapper program. The picture also shows a “heat map” of signal strength. As you can see, there is no rigid dependence - the “field” does not have the shape of a circle, however, the location of the point under study (Megafon) and other neighboring ones was determined quite accurately.

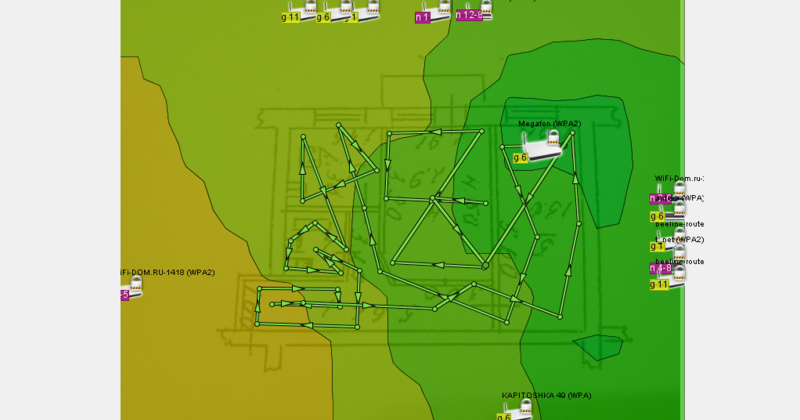
The points that connect the lines can be considered our points, for which the weight and coordinates are known.