Determining the location of a set of vectors in a set of points?

Question

Mathematics

Good day to all. The topic is more mathematical, anyway.
In general, there is some space of points. For example, a map of objects on the floor - there are about 20 cubes on the floor, the exact location of each of them is known.
An observer (H) is located at some point (x, y) of this room. The observer does not know his coordinates in the room. The observer knows his angle of rotation about the north-south axis.
The observer sees 5 cubes, measures the exact distance to each of them. Thus, the observer receives a set of vectors from himself to each cube he sees, knows the length of each vector.
Question: How can an observer determine his coordinates (X, Y), using known data on the position of ALL the cubes of the room, given a set of vectors? At the same time, the observer does not know which cubes he sees (does not know the numbers of the cubes, i.e. he cannot determine exactly which vector points to which cube).
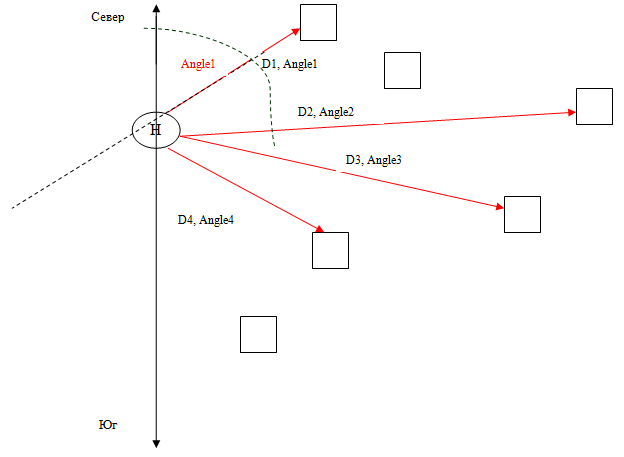
UPD1: Below is a picture illustrating the situation. The cubes are the known points, D ₁ -D _x are the measured distances from the observer (H) to the points. Angle ₁ -Angle _x - vector rotation angles relative to the North-South axis.
UPD2: The theoretical task is to find the location of H (observer) with known D _x , Angle _x , known coordinates of each point.
Moment 1: The observer does not know exactly which points he measured the distance to (does not know their global coordinates), he only knows their location relative to himself (local coordinates in a coordinate system with the observer as the center.
Moment 2: All measurements are carried out in a two-dimensional coordinate system ( in 3D mat. costs will be too high)
.

The practical task is to find the location of the robot in the room. The map of the room is known (the coordinates of all obstacle points at the height of the robot sensors), the measurement results are obtained (with a laser line sensor or by several point measurements with a conventional sensor with a change in the angle of rotation of the sensor), you need to determine your position. The task is complicated by the fact that there will be a lot of points in the room map (even taking into account the low resolution, i.e. 1 point per 10cm, for example), a simple enumeration of all options will take a lot of time.
What option did I have:
1) Calculation of all possible relative vectors from each point to each point of the map (taking into account the distance, i.e. we calculate vectors only for points, the distance between which is not more than a meter). Let's call them global vectors.
2) Calculation of all possible vectors between the measured points (we know their coordinates in the local coordinate system, we can calculate relative vectors. Let's call them measured vectors.
3) Enumeration of measured vectors.
3.1) Any matching global vector for the measured vector is found (direction and length match), fixed.
3.2) The next measured vector is selected, its position relative to the previous measured one is calculated, then the global vector is searched, located also relative to the previous fixed global one.
3.2.1) If the global vector is found, then it is fixed, go to step 3.2
. 3.2.2) If the global vector is NOT found, the results are discarded, go to step 3.1.
3.3) When all the measured vectors are enumerated and a combination of global vectors corresponding to the measured ones is found, then we calculate the coordinates of the measured points based on the found global vectors.
3.4) Well, the calculation of the observer's location point, when the coordinates of the measured points are known, is already a simple geometry.

Answer 1

If there are a lot of cubes and they are located rather chaotically, then based only on the knowledge of the coordinates of the cubes and the vectors of distances from the observer to each cube, it is quite possible to determine the coordinates of the observer.
I solved an approximate problem to determine the rotation and shift of the image of the starry sky.
But the complexity here is quite high: you will need to go to the coordinate system of one of the cubes, build the position vectors of all other cubes relative to the given one based on the observer vectors, and then, by enumeration of the relative vectors known from the positions of the cubes, identify.
As a result, we will be able to accurately obtain the coordinates of the observer.
By the way, in some ways this task is similar to GPS triangulation (only the “cubes” in this case are identified in advance, but instead of vectors we have only lengths).

Answer 2

I'm doing exactly this task right now. Under these conditions (a small base of reference points and a fairly well-known position of several of them in the observer's coordinate system), it can be solved as follows.
1 (preprocessing). For each point from the base, we determine the distances to the remaining 19 points, and sort the resulting vector. We get 20 vectors LB[20][19].
2. For visible points, we do the same - we get 5 vectors of sorted distances LS[5][4].
3. For each pair “vector from LB / vector from LS”, we determine the measure of how much the second vector is a subset of the first - for each element of the second vector, we look for the nearest element of the first and find the maximum or sum of deviations.
4. For each vector from LS, we take the nearest (in the sense of the measure given in (3)) vector from LB. Received the first candidate for matching points. We check whether the distances correspond to each other, and if so, we try to find the transformation of the coordinate system. If the visible points coincided with the base with good accuracy, then we were lucky.
If not lucky, then there are two ways.
5a. We begin to view not the best matches, but the ones following them (by some kind of dynamics). In the end, we'll be lucky - we have only 5 indexes to iterate over.
5b. We choose a vector from LS whose correspondence with a vector from LB was the most reliable in the sense that the second best match (of the same vector from LS but with a different vector from LB) is much worse. We say that the most reliable match is correct, i.e. one cube we learned. We correct the correspondence measure by adding a new criterion - the distances to the found cube must match. After that, we again choose the most reliable match, and so on. Most likely you will.
If you are unlucky, you will have to increase the complexity - for example, compare not the distances between pairs of points, but the shape of triangles. But I hope it doesn't come to that.

Answer 3

Your task is curious, among other things, because of its unconventionality: the exact distance to the "cubes" is known, their exact position, but they are indistinguishable from each other. Usually, in positioning tasks, the opposite is true: the station ID is known (GSM cell ID, Wi-Fi MAC), but the distance to it can only be roughly estimated (by signal strength or propagation time), and where it is located is not at all clear.
So, the input data: a map of the location of the cubes, and a set of five distances x ₁ ...x ₅ to some of these cubes (albeit with some accuracy ±Δ).

1. We take a map, put a transparent layer on it (in terms of graphic editors).
2. We take the first distance from the set, x ₁ , and draw a solid ring around each cube on the map with an inner radius x ₁ -Δ and an outer x ₁ +Δ.
   The rings represent the set of all possible user positions based on a single measured distance.
3. We impose one more layer, we draw rings for x ₂ ±Δ.
4. We merge this layer with the previous one using the AND operation, that is, we find the intersection of the sets. The result will be a set of possible user positions given the two measured distances.
5. Repeat steps 3-4 for x ₃ ...x ₅ .
6. The resulting image shows the possible positions of the user, taking into account the five measured distances. It is likely that there will be several such provisions, which means that the problem did not have an unambiguous solution. It is also possible that the result will be an empty set, in which case it is worth increasing the value of Δ.

Of course, calculating the intersection of the rings is not a particularly fast task. Therefore, each ring can be replaced by a pair of squares (inscribed and circumscribed) - and the whole task will be reduced to finding intersections of rectangles. And even the microcontroller will count this for a dozen cycles :)

Answer 4

This is a common problem when combining camera perspective and 3D scene. camera matching.
Yes, you need 5 known points (cubes) to calculate the coordinates. observer, but it is desirable that they do not lie in the same plane. There should be an implementation for it in a blender or scripts, I would dig there.

Answer 5

And, by the way, if both the relative coordinates of the lighthouses and the north-south direction are known, then everything is generally simple. For each “beacon from the base - visible beacon” pair, our position is calculated for the case if they correspond to each other, after which the densest 5-point cluster is determined in the resulting cloud of 100 points (the problem has been discussed here at least three times lately) .

Answer 6

Implemented the algorithm proposed by DankoUA in this post. It worked right away the first time, which was a little confusing) The position is determined very quickly, it grows, of course, in proportion to the number of points on the map, but this is without optimizations. Accuracy - 95%. I'm a bit down on something - the first implemented algorithm works on the first try and gives accurate results)

Answer 7

If he does not know which vector points to which cube, then in my opinion he does not have a binding to the coordinates of the cube and therefore he cannot determine his location.

Answer 8

Maybe. You can calculate the set of all possible combinations and eventually get the right one, but the price of this algorithm is not even O to the power of N, but something worse. There are similar algorithms in mathematics, but I can’t remember ...

Answer 9

corners are not a problem. The vectors are known - the direction and distance are known. those. you can determine the angle between the vectors, because they all start at the same conditional point (0,0) relative to the observer.

Answer 10

you will have to do m membership checks, taking each point of the grid sequentially as a count. And do not forget about fuzziness - the check should not be accurate, you need to make an allowance

Answer 11

If there are not insanely many vectors between potentially visible cubes (for example, if there are many rooms on the map, but there are not very many cubes in each room), then the whole problem can be solved faster than in O(n). We take a uniform grid, but put in it not the coordinates of the cubes, but the vectors between them (the numbers of the two cubes and the vector). Most likely, even hashing is not needed - there will be a densely filled two-dimensional array of lists. We take any vector between two visible cubes, find the corresponding list of vectors between the base cubes, and follow it. For each pair from the list, we find the position of the observer and perform steps (6,7) from the DankoUA algorithm (i.e., we also need a grid with cubes).

Answer 12

Since we know the orientation of both coordinate systems (i.e., the north-south direction), the task is greatly simplified.
I can offer the following options:
1. Geometric - by means of a cross-correlation function (CCF). Its essence is as follows: the coordinate grid of the positions of the sensors is quantized according to some specific level, and each sensor on it is represented by one pixel. We get the base image. Based on the measurements of the observer, we get a similar (but small) image - the standard. The reference is essentially part of the base image. It remains for us to find the position of the standard on the base image. To do this, we construct the CCF and, from its maximum, with an accuracy up to a quantum of distance, we obtain the displacement of the observer. To clarify it is already the simplest task.
This option will be the more profitable, the more points we have (because it does not depend on the number of sensors, but on their placement).
2. Analytical. This option is highly dependent on the number of sensors. Let N be the total number of sensors and M be the number of sensors seen by the observer.
2a. First, find the location of two randomly selected points from the detected sensors on the common field (there may be several such positions == k); then, by enumeration, identify the remaining points in order to unambiguously determine what kind of sensors the observer spotted. Here you can either "stupidly" sort through all the vectors, choosing one of the points as a base, or go the other way: "draw" an arbitrary vector "drawing" passing through all the detected points (so that each point is connected to one or two adjacent ones), then run through all N points in search of the first suitable match (i.e. if the sum of the position of the i-th point and the 0-th vector of the “pattern” gives the position of another point, we consider that a match has been found), then, substituting 1st vector to the second point found, looking for the third. If it is found, look further. No - we continue the search in search of the 0th vector. And you can make a “drawing”, also taking one of the points found as a basis, but drawing vectors to the rest of the points from it. This will reduce the rounding error of the coordinates (which can give false matches in the case of passing along the “pattern”-trajectory).
2b. Build in advance ordered (say, by angle or distance) arrays of positions (in polar CS) of sensors relative to each other. Get N arrays of (N-1) vectors. Based on the detected sensors, we build a similar array, but one: taking any of the detected points as a reference. Next, we just need to compare our array of (K-1) vectors with N arrays.
This operation can be accelerated if we again quantize (say, by angle): we build N pseudo-histograms, say, in 10-degree increments (we get a pseudo-histogram of 36 "columns"), each cell of the pseudo-histogram will be an array of lengths of vectors that have an angular coordinate in the given interval, or NULL if there are none. In this case, the search will have complexity somewhere O(KN). But for unambiguity, a strict non-uniformity of the distribution of sensors is required.