Confused with the order of operations, how to solve the derivative of a complex trigonometric function?

Question

Mathematics

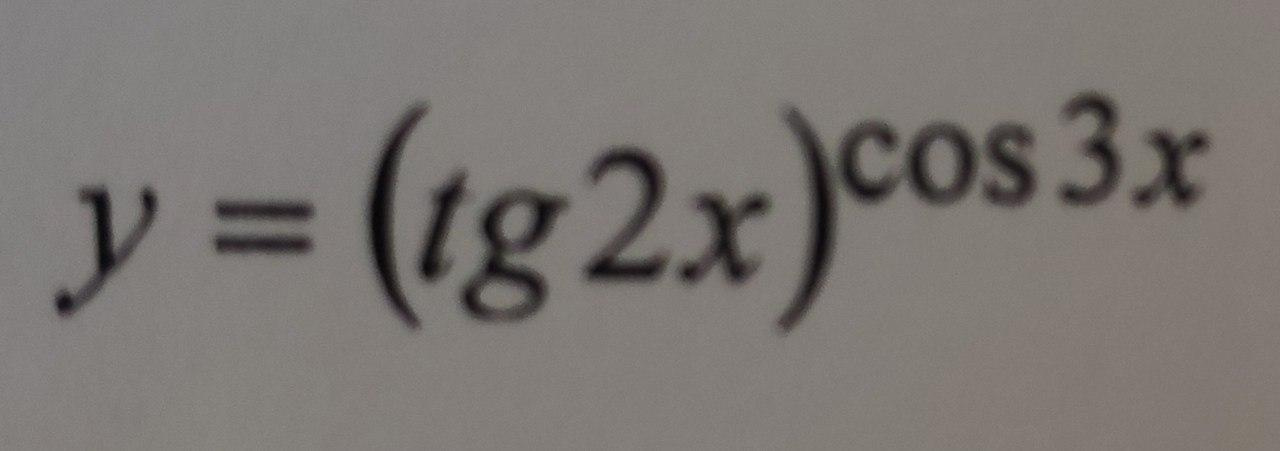
I do this: first I calculate the derivative (tg2x)`, I got 1 / cos ^ 2 (2x),
after which I probably need to act according to the formula a ^ x, but here I get confused and some kind of abracadabra turns out.
Similar tasks are not googled, so I ask you to help with the solution.

Answer 1

Use the standard formula for the derivative of the superposition of functions, first write down where is which function and everything y You separately have 5 functions
a(x) = 3x
b(x) = cos x
c(x) = 2x
d(x) = tg x
e(x) = d(c(x))^b(a(x))
count d(c(x)), b(a(x)), and lastly e(x)

Answer 2

There is a handy trick f(x)^g(x) = exp(g(x) * ln(f(x)), then it is very easy to calculate the derivative:
[f^g]' = exp(g * ln(f) * [g * ln(f)]' = ( f^g ) * ( g' ln(f) + g f'/f )