complex probability. How to implement the generation of a random coefficient according to the schedule?

Question

Mathematics

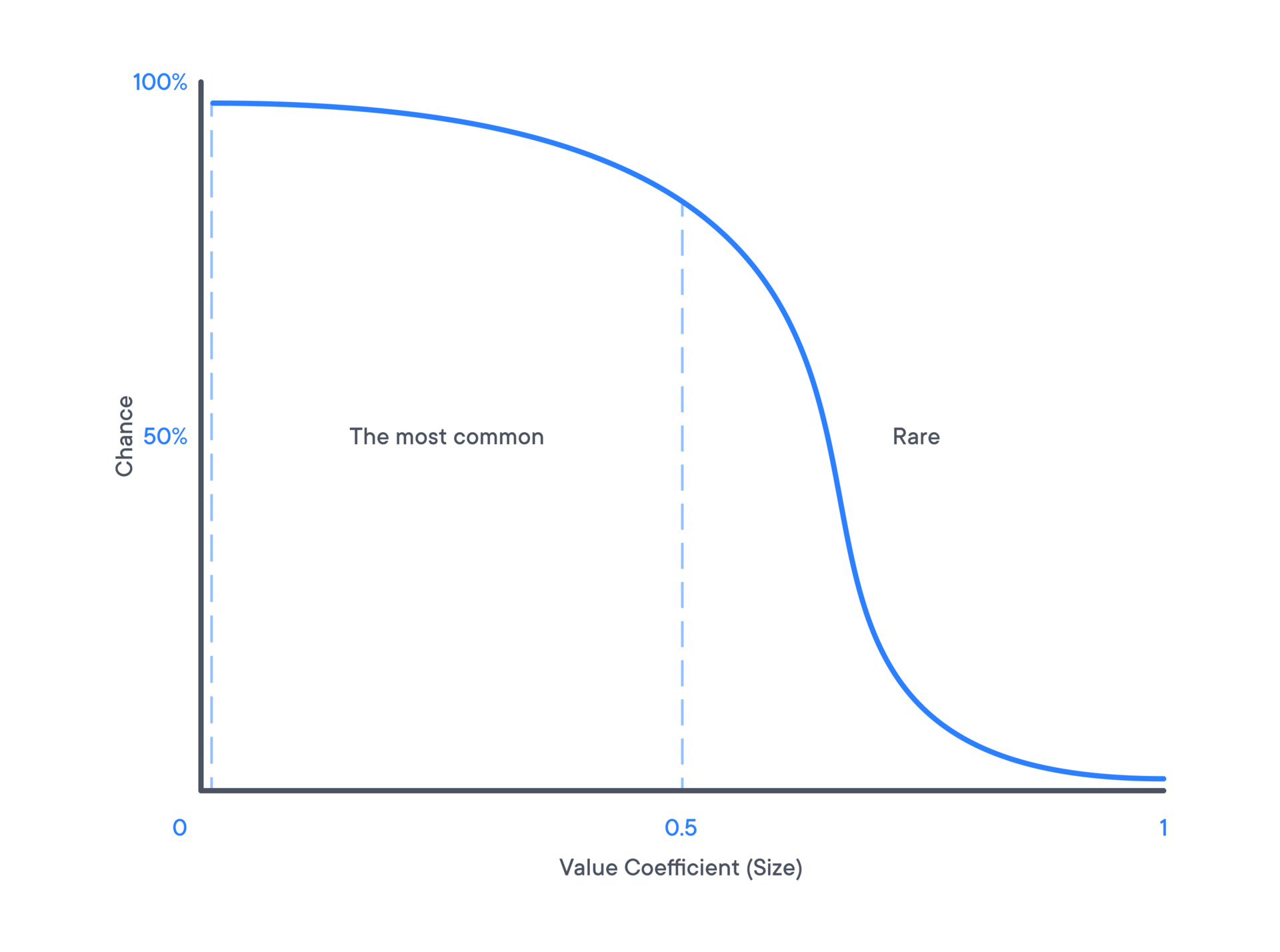
I came across an interesting problem for which I would like to have a solution. I need to get a random number by a coefficient ( min + abs(max - min) * coef), but not just a random number, the randomness of this number will match the graph. Let's say that the random number most often gives out a coefficient less than 0.5, and less often more than 0.5. I have provided an illustration of the graph below. How can this be implemented? (Please give examples in the form of code, or in the form of an explanation of the algorithm)

Answer 1

It all depends on whether you know the formula of your function (quasi) distribution density. I hope that y=F(r) is known, and, accordingly, the function Ф(y)=r, inverse to it, is also known. Then there is no need to reinvent the wheel, everything has been invented before us.
For example: stratum.ac.ru/education/textbooks/modelir/lection2...
On your fingers:
Generate a uniformly distributed number in the range from (according to your drawing) 0 to 100%. You get a point y on the Y axis. Then you calculate r=Ф(y). The sequence of such points {r} will be generated randomly, in strict accordance with your distribution law.
Not just "more often" - "less often", and precisely in accordance with your law.
This is how everyone always does it. Implementation in Python - in three lines.

Answer 2

the randomness of this number will match the schedule.

It is necessary to compose a polynomial of this dependence. That is, this graph itself.

Let's say that the random number most often gives out a coefficient less than 0.5, and less often more than 0.5.

The next step is the probability of dropping one of the parameters (on one of the 2 axes).