Calculation of rotation angles between two coordinate systems

Question

Linear algebra

There is an orthogonal three-dimensional coordinate system (OXYZ). There is another orthogonal coordinate system (OX`Y`Z`), rotated relative to the first one by unknown angles. The centers of the coordinate systems are the same. In the coordinate system (OXYZ) we know the coordinates of the vector OX` and the vector OZ`. It is necessary to find the rotation matrix for the transition from the coordinate system (OXYZ) to (OX`Y`Z`). Help me, I broke my whole brain. Or tell me which way to dig.

Answer 1

OMG, shocked by the answers about quaternions))
If the coordinates in XYZ
OX' = (x1, y1, z1)
OY' = (x2, y2, z2)
OZ' = (x3, y3, z3)
Then the transformation matrix from XYZ to X`Y`Z`
x1, x2, x3
y1, y2, y3
z1, z2, z3
Actually almost by definition

Answer 2

Sorry if I'm wrong now, but you will have two rotation matrices. Around the X axis and around the Y axis. Here they are:
Around X:

Around Y:

Well, finding the angles of rotation is elementary:

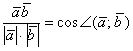
After all, you have the coordinates OX` and OY` in the original system.

Answer 3

Yes, a certain William Hamilton also racked his brains, along with his colleagues. True, it's not about that. But they did something that will also come in handy for us: en.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D1%82%D0%B5%D1%80%D0%BD%D0 %B8%D0%BE%D0%BD%D1%8B_%D0%B8_%D0%B2%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D0%B5_ %D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%B0

Answer 4

As far as I can remember, if we take the coordinates of the orts of the new system placed in the old one, then these coordinates will be the rows of the desired matrix.

Answer 5

Here, the use of Euler angles, matrices and quaternions is described in detail and in an accessible language: www.rossprogrammproduct.com/translations/Matrix%20and%20Quaternion%20FAQ.htm

Answer 6

Take a look here, it might help.
Stewart Platform Math