C#. How to minimize a function that contains sums?

Question

Algorithms

What method and what library can be used to minimize a function in which there is a sum and at the same time there are restrictions on x?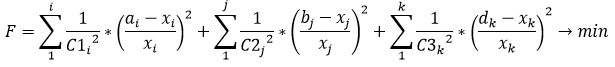

с1-с3, a, b, d - constants, for each x there is a restriction on the minimum and maximum values ​​(x min<=x<=x max).
I tried to use the accord library (methods of Nelder-Mead and Levenberg-Marquardt), but it is impossible to set restrictions there, and it is not entirely clear how to describe the sum in the function.

Answer 1

Judging by the form of the function, your task falls into three simpler ones.
Since there are three blocks of sums in the function and in each block of sums the summed values ​​go to an even degree (degree = 2), then the value of each of the sums is strictly positive.
And if so, then minimize each of the sums separately.
Now, if we take each of the sums separately, it is clear that to minimize the values ​​of the coefficients C are not important, you need to minimize the result of the expression in brackets.
If we take the expression in brackets, then for it the minimum will be for the case when
a(i)=x(i), b(j)=x(j), d(k)=x(k), i.e. for those a(i), b(j), d(k) that fall within the range x min<=x<=x max, the
bracket value will be minimal and equal to zero.
For the rest of the values, the function of the form (a/x)^2 has no extrema, which means that it takes the maximum and minimum values ​​at the border of the range x min<=x<=x max, i.e. either for x = x min, or for
x = x max.

Answer 2

Analyze manually first, then hammer the functions into the program. For example,
i,j,k,c1,c2,c3,a,b,d=1
Then F(x)->min, |x=1
Pay attention to the sum and the squares, as well as the function y=1 /x.