A "new" approach to recursion?

Question

Python

The question arose in connection with the implementation of the well-known Hofstadter function in Python
using memoization. But you can start with the usual Fibonacci numbers.
Define:
F(n) = F(n-1) + F(n-2)
What is wrong with this definition? There are no initial conditions here!
It turns out that we start with an empty dictionary memo_dict = {}
And if we start with n = 1, then the first query F (n-1) will give an error KeyError.

Yes, but we have method overloading! Let's rewrite __missing__it so that when a request for a non-existent key does not throw an error, but it would be assigned a certain default value, say 1.
Thus, the first call to the function will require a forced addition to the dictionary {-1: 1, 0: 1}
Recursion will in a sense “dive into the unknown”, but then everything will continue naturally! The calculation of each new value will use the already created dictionary. The depth of "diving" into uncertainty will be equal to 2.

Now let's turn to QHofstadter
Q(n) = Q(n - Q(n-1)) + Q(n - Q(n-2))

Starting with an empty dictionary, n = 3 and default = 1, everything will happen the same as for Fibonacci: there will
be classical initial conditions {1: 1, 2: 1} and then everything is according to plan.

I'm very curious if there are any articles and studies about this approach to recursion?

The fact that it is not trivial can be easily seen on the example of the same QHofstadter.
Let's start with the dictionary {1:2, 2:1}. In the third step, the recursion will "dive" to the undefined key 0, but then it will again go forward on its own. Trying other, small integer initial values, we will see a wide variety of examples of "diving into the unknown":

{1: 5, 2: 6}

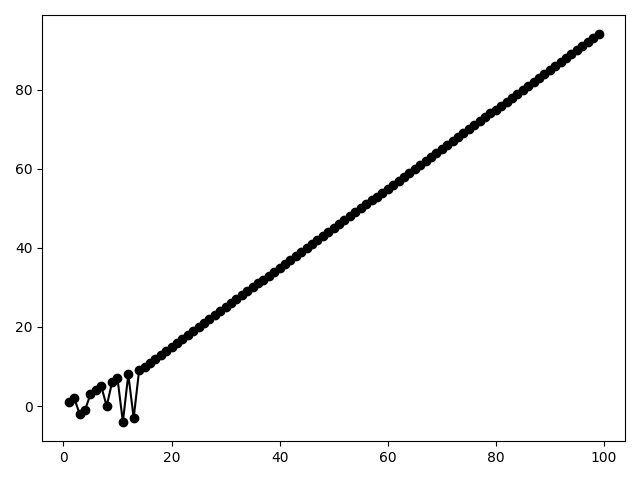
{1: 4, 2: 5}

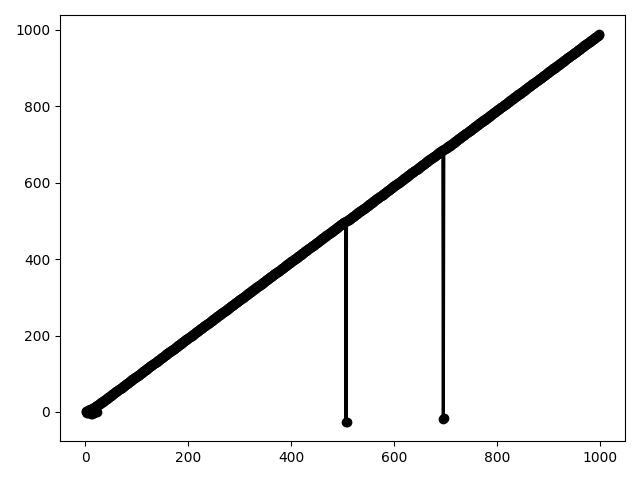
{1: 8, 2: 3}


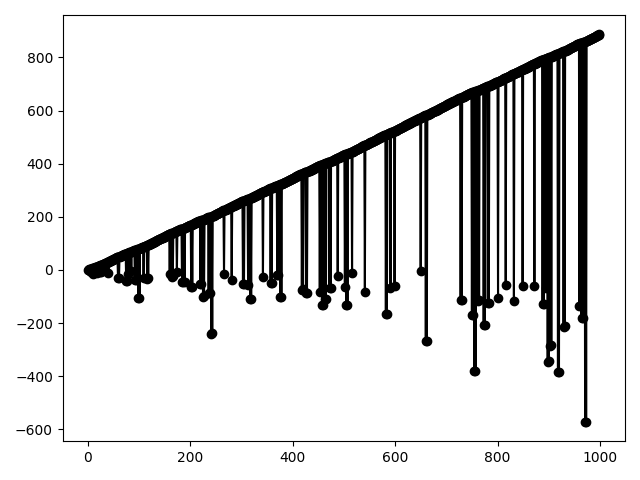
I would like to continue research, but perhaps this topic has long been disclosed.
I would appreciate any comments and links!

Answer 1

No, the approach is not "new".
The author, I will give advice on the presentation of large texts (not literary, but on the case).

• The name should not contain intrigue, but be as clear as possible.
  
• The first paragraph should have an introduction, which reveals the topic in even more detail and explains what will happen next (but not partially, but completely). You don't have to start from afar. It's just a generalization, an abstract level of what comes next. That is, you need to start with the main thing, with an explanation of the essence.
  
• In the last paragraph, approximately the same as in the first, that is, also a generalization, only from the position of completion (from the position of conclusions).
  
• And taking into account the specifics of this resource, it is better to put the middle part under a spoiler if there are more than 2 paragraphs. It is better to publish large articles elsewhere, but the same order of presentation will be needed.
  

Answer 2

Something painfully similar to the delirium of an inflamed consciousness.
In any, absolutely any recursive algorithm, there are conditions for the completion of the recursion, under which the algorithm returns a special statically predefined value.

But you can start with the usual Fibonacci numbers.

In the case of a recursive implementation of the Fibonacci series, this is the condition n<2 and the special value 1 . It's funny, but Hofstadter's condition and special meaning are exactly the same.