Why is the neural network not learning (Backpropagation)?

Question

Python

I'm starting to study neural networks. My neural network needs to learn how to multiply 2 numbers, but for some reason the squared error of the output layer starts to increase with the increase in the number of epochs, and the final result of the output layer tends to 1 all the time. What am I doing wrong? I am attaching the python code and the neural network diagram.

Scheme

Python 3 code

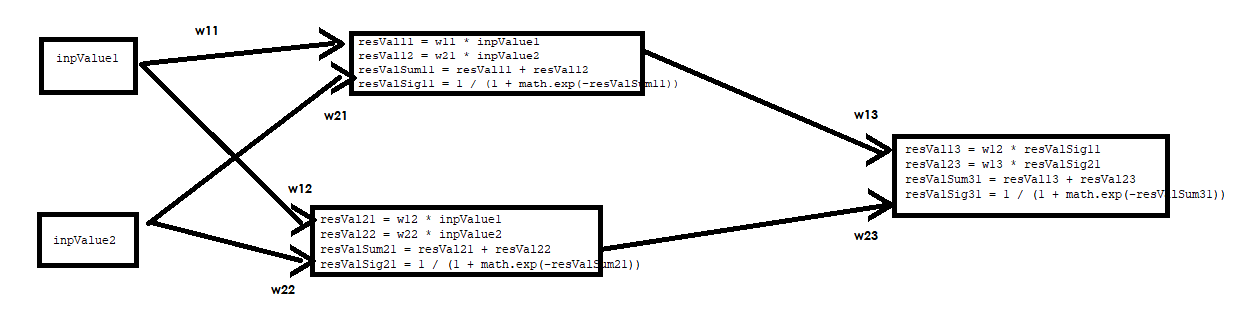
#нейросеть пытается научиться перемножать 2 числа

import random
import math

#learning rate
lr = 0.5
#epoches
epochs = 100

#генерируем два случайных числа

inpValue1 = 0.5
inpValue2 = 0.5

print("Inp Val1:" + str(inpValue1) + " Inp Val2: " + str(inpValue2))

#перемножаем их и выводим правильный ответ
trueVal = inpValue1*inpValue2
print("True Val: " + str(trueVal))

#генерируем начальные веса
#веса на скрытый слой
w11 = 0.45
w12 = 0.28
w21 = 0.36
w22 = 0.75

#веса на выходной слой
w13 = 0.14
w23 = 0.40

print("Start weights w11:" + str(w11) + " w12: " + str(w12) + " w21: " + str(w21) + " w22: " + str(w22) + " w13: " + str(w13) + " w23: " + str(w23))

#запускаем нейросеть и обучаем ее
e = 1
while e < epochs:

    resVal11 = w11 * inpValue1
    resVal12 = w21 * inpValue2
    resVal21 = w12 * inpValue1
    resVal22 = w22 * inpValue2

    #суммирование для сигмоиды
    resValSum11 = resVal11 + resVal12
    resValSum21 = resVal21 + resVal22

    #резултаты на входе после сигмоиды
    resValSig11 = 1 / (1 + math.exp(-resValSum11))
    resValSig21 = 1 / (1 + math.exp(-resValSum21))


    #отправляем значения в выходной слой
    #умножаем данные на веса
    resVal13 = w12 * resValSig11
    resVal23 = w13 * resValSig21


    #суммируем для сигмоиды
    resValSum31 = resVal13 + resVal23

    #результат нейросети
    resValSig31 = 1 / (1 + math.exp(-resValSum31))
    resValSig31 = float("%.3f" % resValSig31)

    print("NeurVal: " + str(resValSig31) + " TrueVal: " + str(trueVal))

    #распространение обратной ошибки

    #ошибка выходного слоя
    errValO = trueVal - resValSig31
    errValO = float("%.3f" % errValO)
    sgrErr = errValO * errValO
    sgrErr = float("%.3f" % sgrErr)

    print("Output error: " + str(sgrErr))

    #обновление весов от скрытого слоя к выходному
    #дельта весов
    deltaWO = errValO * (resValSig31 * (1 - resValSig31))

    #новые веса
    w13 = w13 - resValSig11 * deltaWO * lr
    w13 = float("%.3f" % w13)
    w23 = w23 - resValSig21 * deltaWO * lr
    w23 = float("%.3f" % w23)

    #ошибка скрытого слоя
    errValH11 = w13 * deltaWO
    errValH21 = w23 * deltaWO

    #дельты весов скрытого слоя
    deltaWH11 = errValH11 * (resValSig11 * (1 - resValSig11))
    deltaWH21 = errValH21 * (resValSig21 * (1 - resValSig21))

    #новые веса скрытого слоя
    w11 = w11 - inpValue1 * deltaWH11 * lr
    w11 = float("%.3f" % w11)
    w12 = w12 - inpValue1 * deltaWH21 * lr
    w12 = float("%.3f" % w12)

    w21 = w21 - inpValue2 * deltaWH11 * lr
    w21 = float("%.3f" % w21)
    w22 = w22 - inpValue2 * deltaWH21 * lr
    w22 = float("%.3f" % w22)


    print("New weights w11:" + str(w11) + " w12: " + str(w12) + " w21: " + str(w21) + " w22: " + str(w22) + " w13: " + str(w13) + " w23: " + str(w23))

    e = e + 1
    print("End of epoch " + str(e))

Answer 1

Errors:

1. an attempt to train the network on just one sample;
   Try to start by training the network with a function of one variable, for example y = A * x^2 + BPrepare a dataset of one hundred thousand points (x, y)
   upd for training it . here they write that their network converged only on configurations 2-4-1- with two hidden layers with 2 and 4 neurons.
   upd. 2 tried to implement multiplication by a two-layer network. You can play online .
   Keras , numpy .
   
   The code

   # import libraries
   from keras.models import Sequential
   from keras.layers import Dense
   import numpy as np
   
   # определяем модель
   model = Sequential()
   model.add(Dense(units=2, activation='relu', input_dim=2))
   model.add(Dense(units=4, activation='relu'))
   model.add(Dense(units=1, activation='relu'))
   
   model.compile(optimizer='adam', loss='mean_squared_error', metrics=['accuracy'])
   
   # создание набора данных
   def create_data(n):
     values = np.random.random_sample((n,2,))
     labels = np.prod(a=values, axis=1)
     return values, labels
     
   # тренировочные данные и тренировка модели
   values, labels = create_data(1000)
   model.fit(values, labels, epochs=10, batch_size=10)
   
   # тестовые данные и как посчитает их модель
   test_values, test_labels = create_data(5000)
   results = model.predict(test_values, batch_size=2)
   
   # проверим, насколько ошиблись
   sq_error = []
   for i in range(0, len(test_values)):
     sq_error.append( np.square(results[i][0] - test_labels[i]))
   
   print('Total rmse error: ', np.sqrt(np.sum(np.array(sq_error))))  
   # Total rmse error:  5.101393144138632