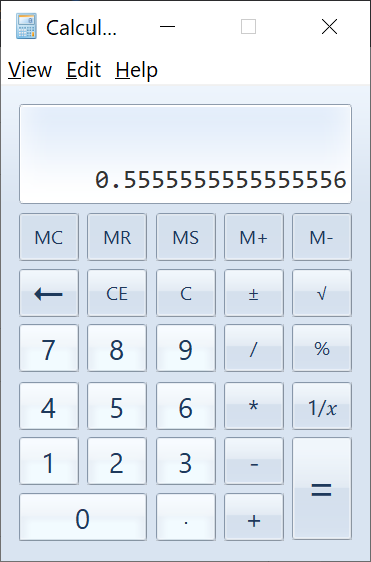
Why is 5/9 divided into 0.55555....6?

Question

Mathematics

In some calculators, for example, on my smartphone, when dividing 5/9, it turns out to be an infinite fraction, but 6 is taken from the end from somewhere.
Is this some kind of rounding, or a problem with the programming language in which they are written?
Why is this happening? For example, in the standard Windows 7 calculator, the problem is absolutely the same.

Answer 1

Always the same remainder after division.
Therefore, an infinite process generates a periodic ( decimal ) infinite fraction.
For the last digit of the number, mathematical rounding is used .

Answer 2

This is a problem with computers in principle - they are finite and cannot store infinite real numbers. Real numbers in a computer are usually limited to 8 bytes (there may be other options). So for anyone, you have to round off infinite fractions, as well as any others that do not fit into the bit grid. In addition, there are other problems arising from the limitations of the computer representation of numbers.
A counter question - how would you display an infinite fraction in the Windows calculator?

Answer 3

The Windows calculator uses a computer double for transcendental operations, and (like electronic calculators, by the way) self-written decimal arithmetic for addition / subtraction / multiplication / division. Well, it’s good - you don’t have to talk about computer (binary) fractional artifacts.
Take and round in the decimal system 0.5555555555555 ... - of course, it will be 0.556. Or 0.5555556 - it all depends on how many digits you want to leave.

Answer 4

School informatics course:
https://www.yaklass.ru/p/informatika/10-klass/info...
This leads to a problem when comparing real numbers with each other:
https://0.30000000000000004.com/
https://stackoverflow. com/questions/588004/is-floa...