Why does the Schottky group look wrong?

Question

Mathematics

With GLSL, I was trying to draw a fractal, which is a visualization of the "Schottky group".
Based on the book "Indra's Pearls. The Vision of Felix Klein.", but the illustrations in it are different from what comes out of me.
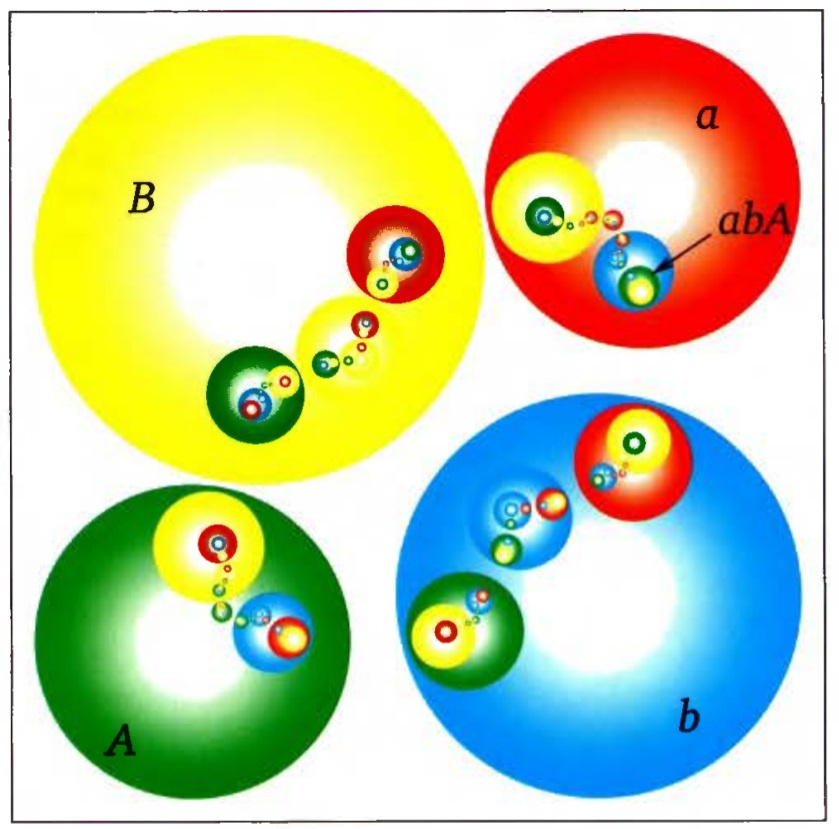
Fractal from the book:

My fractal:


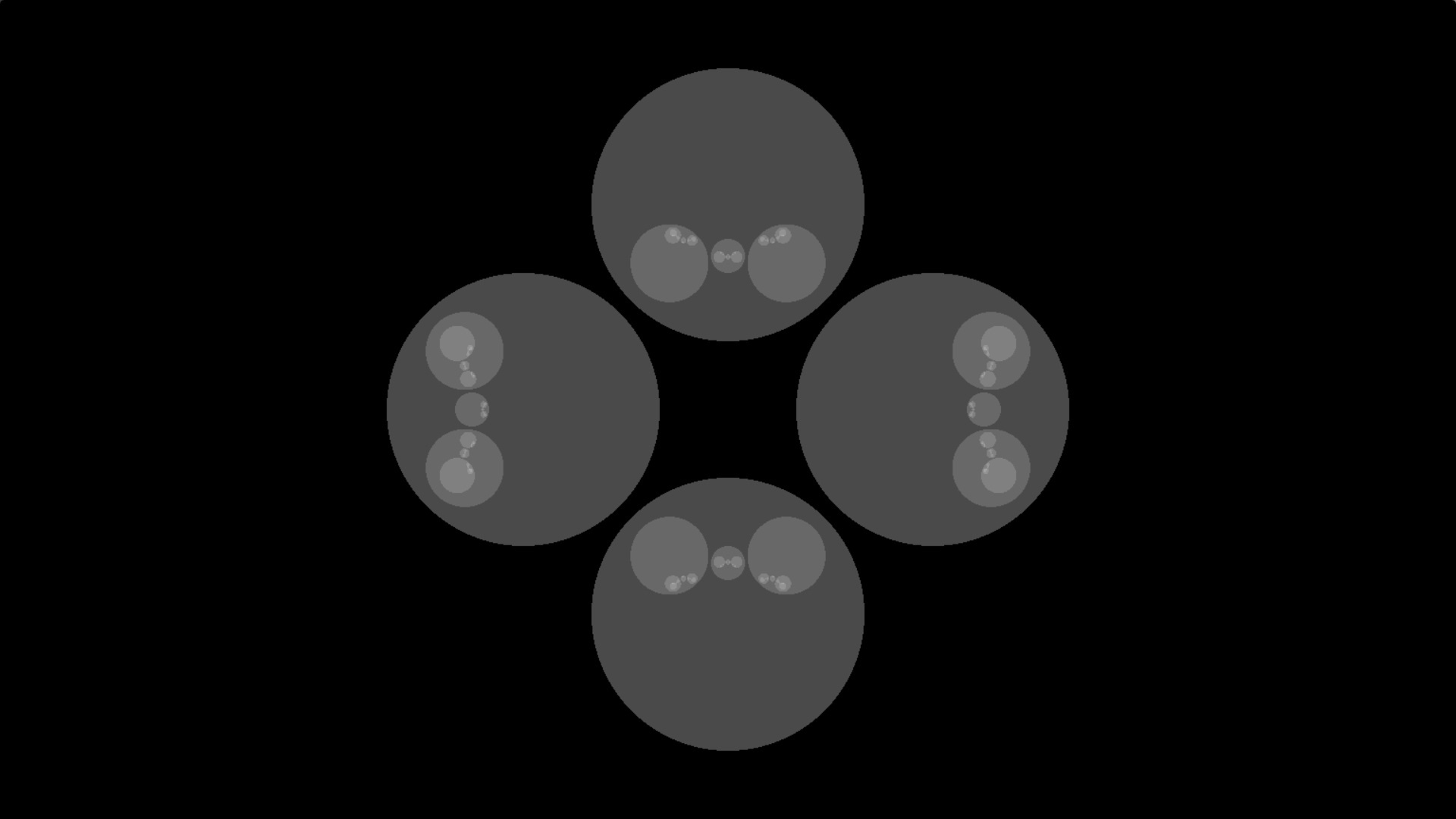
Here is a method that determines the Möbius transformation (based on a pair of generating circles) and a method that determines the brightness of a point depending on its coordinate:

mobius connect(vec2 P, vec2 Q, float r, float s){
    return normMobius(Q, one*r*s-zmz(P,Q), one, -P);    
}
float DE(vec2 z){
    vec2 O1 = vec2(-1.5,0.); float R1=1.;
    vec2 O2 = vec2(1.5,0.); float R2=1.;
    vec2 O3 = vec2(0.,-1.5); float R3=1.;
    vec2 O4 = vec2(0.,1.5); float R4=1.;
    
    mobius A = connect(O1,O2,R1,R2);
    mobius a = connect(O2,O1,R2,R1);
    mobius B = connect(O3,O4,R3,R4);
    mobius b = connect(O4,O3,R4,R3);

    int i=0,I=12;
    for(;i<I;i++){
        if(length(z-O1)<R1){
          z=apply(A,z);
        }else if(length(z-O2)<R2){
            z=apply(a,z);
        }else if(length(z-O3)<R3){
            z=apply(B,z);
        }else if(length(z-O4)<R4){
            z=apply(b,z);
        }else{
            break;
        }
    }
    return sqrt(float(i)/float(I));
}

Also, here is a part of the code that describes the structure of the Möbius transformation ( z -> (az+b)/(cz+d)).

struct mobius{
    vec2 a,b,c,d;
};
mobius normMobius(vec2 a, vec2 b, vec2 c, vec2 d){
  vec2 det = zmz(a,d)-zmz(b,c);
  det = zpf(det,.5);
    return mobius(zdz(a,det),zdz(b,det),zdz(c,det),zdz(d,det));
}
vec2 apply(mobius t, vec2 z){
    return zdz(zmz(z,t.a)+t.b,zmz(z,t.c)+t.d);
}

Also, I will clarify that zmz and zdz are multiplication and division of complex numbers.

So what am I doing wrong? Why do such transformations generate the wrong pattern? How can they be changed?

Answer 1

From the discussion under the question, it became clear that it is necessary that the circles in the pattern touch, i.e. form a coherent structure. For this, it is necessary, firstly, that the original circles touch and, secondly, that the transformation leaves the touch points in place. You can pick up a lot of such transformations, but for example, an inversion transformation that leaves the entire circles themselves in place is suitable.