Answer the question
In order to leave comments, you need to log in
Which geometry is more suitable for a 3D sphere?
I'm trying to generate a sphere with different levels of detail.
The first was a sphere, divided by a quadtree in w / d, but in this way too many parts were obtained for a certain density (which is already talking about the uneven density of the geometry.
The second quadtree geometry is based on a cube, but even there the triangles differ greatly in area (at the corners they are small, large in the middle) 
Then I looked closely at the regular polyhedra:
from the octahedron
I also received triangles that differ in area (they are smaller at the poles) where the face consists of 5 triangles, with the vertex at the center of the face)
Still, which one is better to choose, and what other parameters should be taken into account if you need to break the faces of such a polyhedron into relatively equal parts in order to establish lovel-of-detail ?
UPD: Icosahedron, generated in Blender. 
The closer to the junction of the original faces, the smaller the edges of the triangles after splitting.
UPD:
I understand what's the matter: I
presented the figure in a horizontal cut in the center, where
in green - the places of the cut while maintaining the same length of the edges, guided by the angle (what you need)
in blue - the places of the cut of the face by distance on the same face (linearly)
while I don't know how to state it exactly, but the result is the following 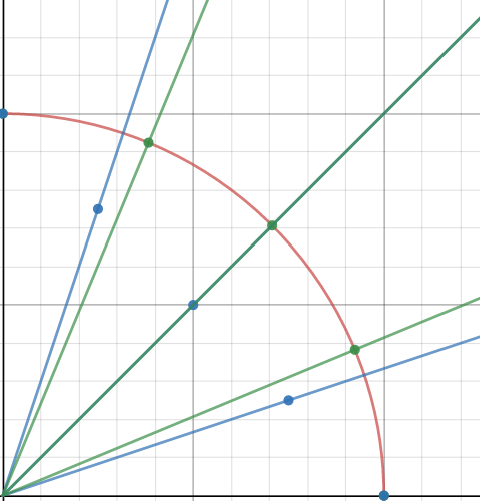
Live example: https://www.desmos.com/calculator/plxwk8mukm
Answer the question
In order to leave comments, you need to log in
As a result, using the example of splitting an octahedron, I got:
UPD: something turned out to be a miscalculation - the area with a radial is still not the same (min area: 0.0192 -> max area: 0.0347)
Green (linear) is a standard way of splitting, it turns out like this that the outermost triangles have a smaller area. Moreover, it is 5 times different from the maximum.
Black - radial subdivision, the area is not so different preserved.
Cause - corner defect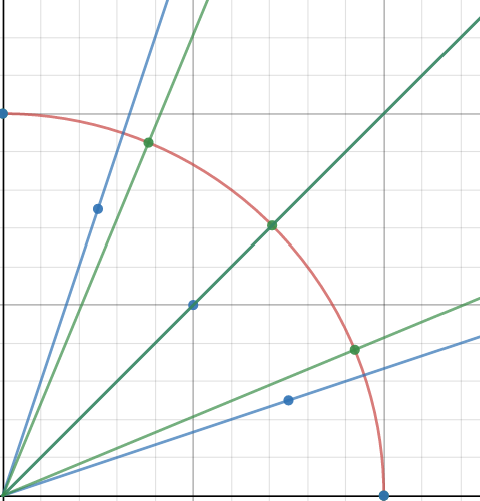
For LOD problems, you are best suited for a sphere of identical equilateral triangles.
But you still need to look at what you want to impose on this area, for certain tasks your first option is more suitable.
Take an icosahedron and do tessellation: instead of one triangle there will be 4 (at the same time, all new and old vertices continue to be inscribed in one sphere, i.e. have the same radius vector). The partitioning continues several times. Frank Luna's book DirectX 12 gives an example of the geosphere.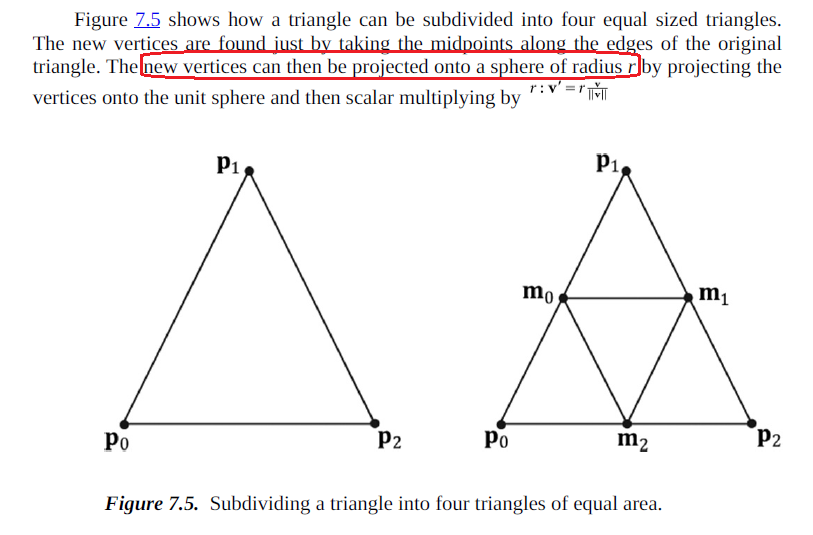
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question