Answer the question
In order to leave comments, you need to log in
What to read to learn how to solve problems on a plane?
When passing the entrance exams, there will be problems like this: 2 parallel planes are given, there is a point that does not lie on these planes, 2 straight lines are drawn through it, so that the straight lines intersect the planes at some different points ... then the lengths of some segments are given and you need to find the length some unknown segment. Something like.
There will be about 30% of such tasks. And I can't decide at all. I do not represent from what topic these tasks.
Please tell me materials, videos, articles, etc. that will help you understand these tasks and with which you can learn how to solve them.
Thank you.
PS. Here is one of the tasks: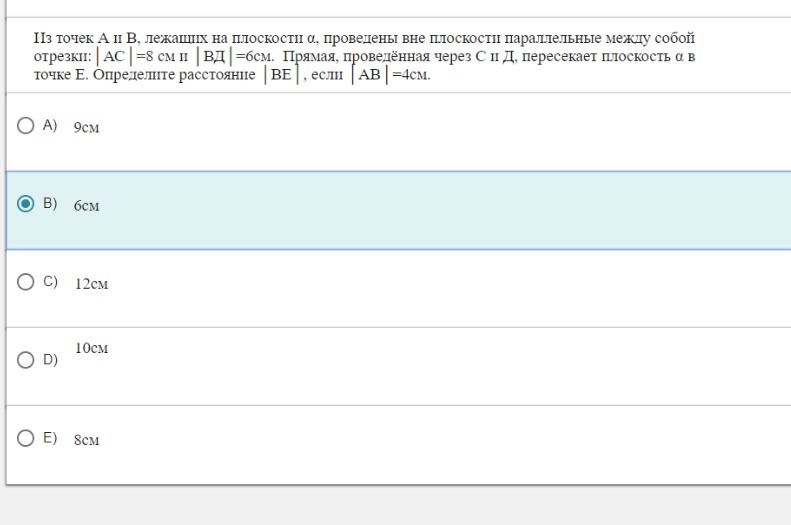
Answer the question
In order to leave comments, you need to log in
You just need to learn to imagine the conditions in your head.
In the given condition, a triangle and a trapezoid at its base are obtained.
It is difficult for some people to imagine (it is not clear why - probably problems with the brain) - in this case, one must immediately abandon the technical path of education.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question