What's wrong with finding the mathematical expectation?

Question

Algorithms

Task:
Word-landia is a new country formed by the unification of two ancient states under the influence of external threats. These states are now provinces of Word-land, but the referenda on their name have not yet passed, so they are called Major and Minor Byte-lands.

To unite the population, it was decided to hold a championship between the provinces. Chess is the national game in the Elder Byte-land, and volleyball is the national game in the Younger. Therefore, the championship was decided to be held in chess. In order not to drag out the championship, the united government decided to hold exactly K matches. Each match is either a game of chess or a volleyball match. The winner of the match receives one point towards the championship, in case of a draw in a chess game, both provinces receive 0.5 points each.

The government is interested in “friendship winning” in the championship, that is, the provinces score the same number of points. Therefore, high officials have asked you to determine the minimum number of chess games in the championship, so that the difference in the mathematical expectations of the points scored by the provinces would be minimal.

It is known from the long history of the World Championships that the Senior Byte-land beats the Junior in chess with probability p1 and loses in volleyball with probability p2. A draw in chess was achieved with probability p3. Note: The mathematical expectation is the average value of a random variable in probability theory. For a discrete random variable X with the distribution law P(X = xi) = pi, the mathematical expectation is the sum of paired products of all possible values ​​of the random variable and their corresponding probabilities, i.e.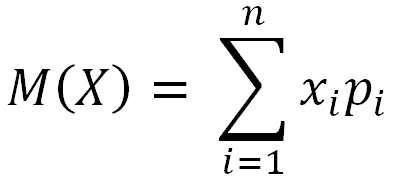

Input:
The input file INPUT.TXT contains four integers: K (1 < K ≤ 10^16), p1, p2, p3 (0 ≤ p1, p2, p3 ≤ 100) – the number of matches and probabilities in percent.

Output:
In the output file OUTPUT.TXT print one natural number - the minimum number of chess games (note that the championship should not turn into a chess tournament).

Examples:
Input:
3 50 50 50
Output:
1

Input:
4 0 0 100
Output:
3

Idea: use the formula and calculate the probability of winning for each team, not needed for a draw because it will be the same for both teams and will decrease when subtracted. It is necessary to count for all the different amounts of playing chess, but it is not possible that only chess is played. Then we display the number of games for which the modulus of the difference of mathematical expectation is minimal.

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>

struct Chess 
{
    long long int number;
    long long int p1;
    long long int p2;
    long long int p3;
    
    long double difference;
};

int main()
{
    long long int aNumber = 0, pos1 = 0, pos2 = 0, pos3 = 0;


    std::cin >> aNumber;
    std::cin >> pos1;
    std::cin >> pos2;
    std::cin >> pos3;

    std::vector<Chess> chess(aNumber);

    for (long long int i = 0; i < aNumber; i++)
    {
        chess[i].number = i + 1;
        chess[i].p1 = pos1;
        chess[i].p2 = pos2;
        chess[i].p3 = pos3;
        chess[i].difference = abs(2 * chess[i].number * (chess[i].p1 + chess[i].p2 - 100) +
                                  aNumber * (100 - 2 * chess[i].p2)
        );
    }

    std::sort(chess.begin(), chess.end(), [](Chess& left, Chess& right) 
        {
            return left.difference < right.difference;
        });

    if (chess[0].number == aNumber)
    {
        std::cout << chess[1].number;
    }
    else
    {
        std::cout << chess[0].number;
    }
}

Answer 1

You have an error in calculating difference. At you there superfluous minuses at line breaks. The compiler does not work with line breaks, as in school in a notebook. Do not put a sign at the end of a line and at the beginning of the next. You only need to put up one sign. The compiler will ignore the line break and see A - - B, which is the same as A+B.
Only after the correction, your solution will most likely not pass in time. Because K is up to 10^16 in the problem and you are iterating up to it.
Transform your formula for difference - take chess[i].number out of brackets. Get something like abs(chess[i].number*A + B).
And you can find the minimum of this linear function in one step - this is -B/A. But this is if the desired number can be fractional. For integers, you need to look at 2 values ​​- rounded decimals down and up. You can get them by doing all the calculations only in integers. And then you need to choose one of the two smaller differences, provided that chess[i].number is not equal to K there.