What is the error of the algorithm (8 Puzzle, A*)?

Question

Algorithms

Stuck with the solution to this assignment on Coursera.
In general, it is difficult to tell all the features here, so I hope someone took this course too.
I practically implemented this algorithm, but this is the problem with some puzzles.
Suppose there is such a board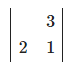
At the first step, two of its "neighbors" are entered into the priority queue.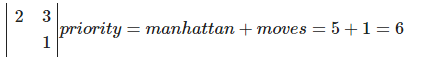

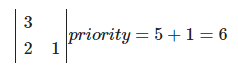
Since they have equal priority, the priority queue, in principle, can be given by anyone, in my case, the first one is taken.
At the second step, one more neighbor of the board just drawn is added to the priority queue (the second one is not added because it is identical to the previous board). In total, it has two boards: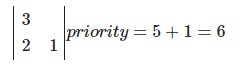

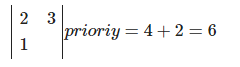
And again, the priorities are the same, so the first one is taken and, as a result, there is already an error in the extracted sequence: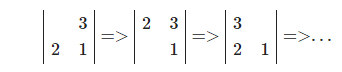

Apparently, I misunderstood something. But some puzzles (where the priorities do not match) are collected normally. What is wrong with my reasoning?
PS I already asked on the Coursera forum, but The course is already ending, there are now quite a few people.
PPS Once again, I did not describe all the details, so the question is designed for those who have solved a similar problem.

Answer 1

As far as I understood from the example in the description of the problem, the algorithm builds the entire decision tree at once, moving in parallel along the most optimal positions in the tree. That is, for each position, it is necessary to store the ancestor, then, after reaching the final position in one of the branches, it will be possible to build the entire chain of moves.

Answer 2

And why, if you go to 3-0-2-1 (the second variant of the first step), do you still have 2-3-0-1 (the first variant of the first step) in the chain? Do you have a SearchNode class with a field, conditionally, previous?
Upd .: or there I can first ask: queue elements of what class?