Answer the question
In order to leave comments, you need to log in
What is it and how to solve it?
It seems like this Second Order Linear Differential Equation is homogeneous, but... what to do with the free term on the right side? and a game on x what to do with it? those. how to decide?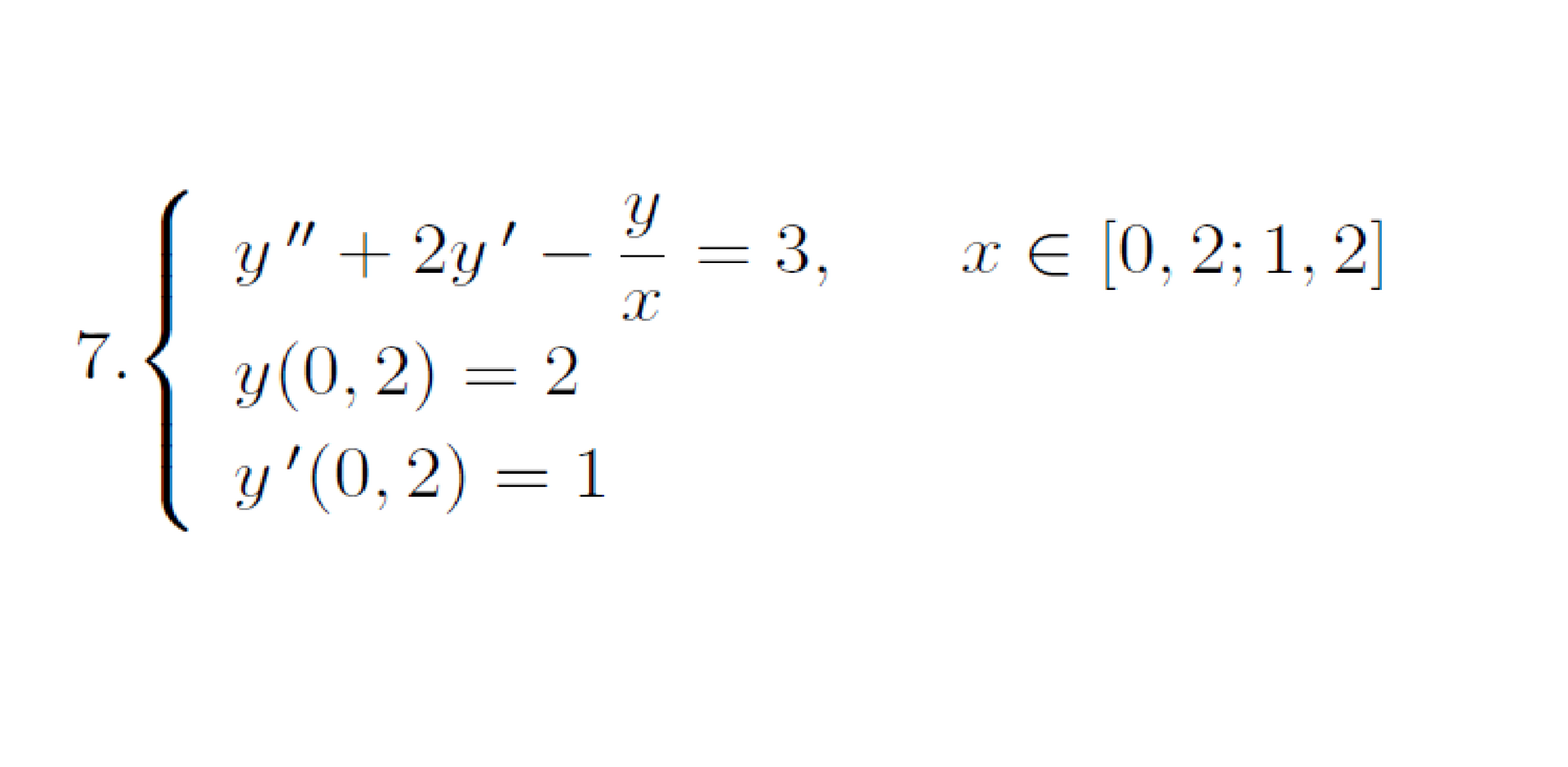
Answer the question
In order to leave comments, you need to log in
We replace the function t = y/x , as well as the variable with z = -2x , after conjuring, we get
zt'' + (2-z)t' - t/2 = -3/2 (where differentiation is implied by z)
We have given equation to the canonical form for the degenerate hypergeometric equation . Due to the right side, it is non-uniform. But as you remember, the general solution of a linear non-homogeneous equation is the sum of the general solution of a homogeneous equation and a particular solution of a non-homogeneous equation.
For the general solution of a homogeneous degenerate hypergeometric equation, see for example here https://dic.academic.ru/dic.nsf/enc_mathematics/92... . Of course, it is given through the appropriate special functions.F(...) .
Next, we need to find a particular solution to the inhomogeneous equation. It is chosen in an obvious way t(z) = 3 .
Putting it all together, we get the final solution:
y(x) = C1 * x * F( 1/2, 2; -2x ) + C2 * F( -1/2, 0; -2x ) + 3x
Substitute the initial conditions and find the integration constants C1 and C2 are already themselves.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question