What does the standard solution of an ellipse look like by center and 3 points?

Question

Mathematics

The bottom line is this:
There is a bar that promises to be of a round section, but in fact the section of this bar is closer to an ellipse, and besides, it also walks along its entire length.
I can take 3 diameter gauges, position them 120 degrees apart from each other (my intuition tells me that this will be enough) and take readings in real time.
With this data, I would like to calculate the area of ​​the ellipse and apply a correction factor. And I would also like to know the maximum diameter / radius of the ellipse in order to warn about the possibility of a bar jam.
Actually a question:
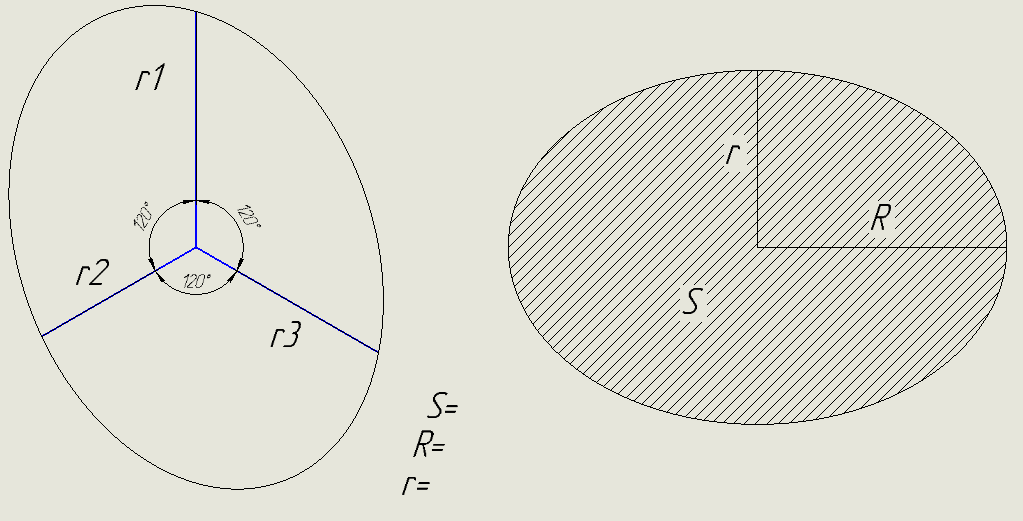
It is necessary to find the area of ​​an ellipse, the minimum and maximum radius.
Knowing r1, r2 and r3 and the angle between them.

Answer 1

TLDR:

S = Pi*sqrt(3 / [ (1/L1+1/L2+1/L3)^2-2*(1/L1^2+1/L2^2+1/L3^2) ])

here L1, L2, L3 are the squares of three dimensions.
Formula Derivation:
A little bit of analytic geometry and a lot of elementary algebra will help you deduce these equations.
If you enter a coordinate system with axes along the main radii of the ellipse, then the equation of the ellipse will be:
x^2/a^2+y^2/b^2 = 1
In this case, all points at an angle alpha to the semi-major axis will be on the beam:

x(t, alpha) = t*cos(alpha)
y(t, alpha) = t*sin(alpha)

Let's denote the sine and cosine of the angle for the first dimension as:
s = sin(a1), c = cos(a1)
Let the squares of the distances be L1, L2, L3.
If we intersect the ray and the ellipse, we can formulate an equation for the length along the angle a1 (the first dimension) by simply substituting the known x(a1, sqrt(L1)) and y(a1, sqrt(L1)).
1/L1 = c^2/a^2+s^2/b^2
For other measurements, add 120 degrees to the angle under cos and sin. If you expand cos(120+a1) = cos(120)cos(a1)-sin(120)sin(a1)and sin(120+a1) = cos(120)sin(a1)+sin(120)cos(a1), then you can make 2 more equations:

1/L2 = (-1/2*c-sqrt(3)/2*s)^2/a^2+(sqrt(3)/2*c-1/2*s)^2/b^2
L3 = (-1/2*c+sqrt(3)/2*s)^2/a^2+(-sqrt(3)/2*c-1/2*s)^2/b^2

In total, taking into account the trigonometric identity s^2+c^2=1, we have 4 equations for 4 unknowns a, b, c, s.
But we don't need all the values. The area of ​​the ellipse is Pi*a*b, and the radii of the ellipse are a and b.
By opening the squares above and adding these equations in every possible way, you can end up with

1/a^2+1/b^2 = 2/3*(1/L1+1/L2+1/L3)
1/a^2*b^2 = [ (1/L1+1/L2+1/L3)^2-2*(1/L1^2+1/L2^2+1/L3^2) ]/3

Hence the area:

S = Pi*ab = Pi*sqrt([ (L1+L2+L3)^2-2*(L1^2+L2^2+L3^2 ]/3)

To find the radii of an ellipse, you need to find a and b. Above, two equations have already been given for the sum and product of 1/a^2 and 1/b^2 - you can get a quadratic equation for t=1/a^2 from them. Its two solutions will be your radii of the ellipse (don't forget to take the roots and invert). Here it is necessary to carefully substitute the expressions in the school formulas for the quadratic equation.

Answer 2

Equation of an ellipse centered at (0,0) - ax^2 + bxy + cy^2 = 1
Plug in known points to get coefficients