Answer the question
In order to leave comments, you need to log in
The task of filling the field with puzzles. What are the solutions?
Good afternoon!
There is a field that needs to be filled with puzzles (elements) from a fixed set.
It is necessary to write a program that determines the possibility of filling the entire field with puzzles, i.e. you need to fill the entire field with puzzles (so that there are no empty spaces left).
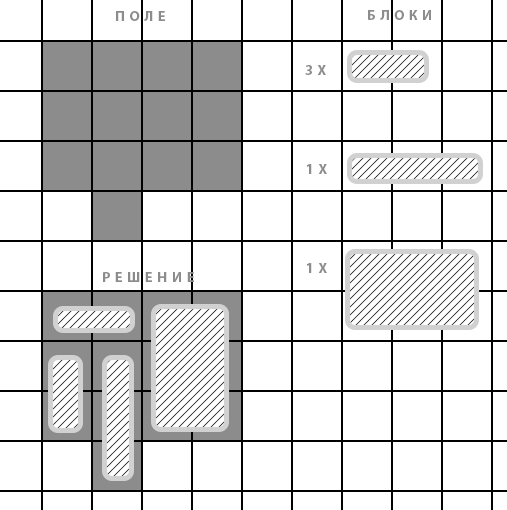
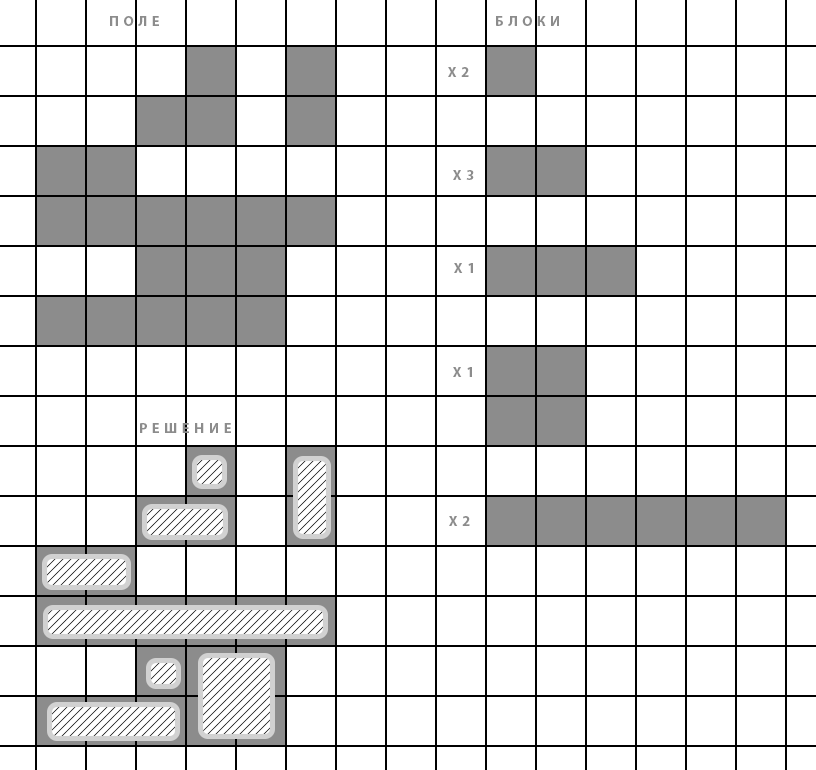
Answer the question
In order to leave comments, you need to log in
sample = (("11", "1 1 2"),
("1111\n1111\n1111\n0100", "2 1 3\n3 1 1\n3 2 1"),
("000101\n001101\n110000\n111111\n001110\n111110",
"1 1 2\n2 1 3\n3 1 1\n2 2 1\n6 1 2"),
("111\n101\n111", "2 1 4"))
class Field:
def flip(self):
self.cells[:] = sorted((x, y) for y, x in self.cells)
self.flipped ^= True
def dismantle(self, cells, flipped):
self.cells, self.flipped = cells, flipped
left, right = cells[0][0], cells[-1][0]
tmp = sorted(y for _, y in cells)
top, bottom = tmp[0], tmp[-1]
h, w = bottom - top + 1, right - left + 1
if w * h == len(cells):
wh = (w, h) if h < w else (h, w)
c = tails.get(wh, 0)
if c:
tails[wh] = c - 1
yield (self,)
tails[wh] = c
for lo, hi in (left, right), (top, bottom):
for i, (x, _) in enumerate(cells):
if lo < x <= hi:
for one in Field().dismantle(cells[:i], self.flipped):
for two in Field().dismantle(cells[i:], self.flipped):
yield [*one, *two]
lo = x
self.flip()
_field, _tails = sample[0]
tails = {}
for s in _tails.splitlines():
w, h, c = map(int, s.split())
if w < h:
w, h = h, w
tails[w, h] = c
for partition in Field().dismantle(
sorted((x, y) for y, s in enumerate(_field.splitlines())
for x, c in enumerate(s) if c == '1'), False):
for f in partition:
if f.flipped:
f.flip()
print(*f.cells)
break
else:
print('не смогла')There is a so-called backpack problem, but I don’t think that it can be applied here. because you need to fit blocks not in a rectangle. it is possible to optimize the enumeration a little, for example, for individual sites (2 decks in the second diagram). in general, such a search is performed quite quickly and optimization makes sense only for large areas.
Backtracking exhaustive search, optimized by refinements:
1. Elements should be sorted from largest to smallest, and repetitions should be discarded during enumeration.
2. Each time, trying on the next element in the next place, check whether it is possible to cover each of the cells of the remaining field with at least one of the remaining elements. Cutting off the meaningless further enumeration.
we did this for a grid of 100*100, the blocks were from 1*1 to the maximum)))
1 nuance - ONE block is added in one stage, while there may already be a certain number of different blocks on the field.
2 nuance - there were still conditions - to place closer to the bottom or closer to the center, etc.
3 nuance - a block or a square or a rectangle, there were no snakes or corners.
but there is all the code in mysql queries, it is unlikely that I will chew it into an algorithm for you ...
offhand - inserting in a block cycle and the result - fit, did not fit, etc.
those. triviality, the whole point is in optimizing a wild number of requests
And in fact - Mike from the stack and someone else from the mysql-forum suggested good algorithms, there are hardly such minds here, sorry, Toaster.
I see the branch and bound method (smart enumeration).
Roughly speaking, when you put a piece on the field, you get the same task, but with fewer elements and with a smaller area of \u200b\u200bthe field. Trying a figure, you can evaluate the availability of a variant according to certain criteria, and if it is still available, continue the procedure recursively.
The algorithm is approximately the following:
1. Choice of figure: any, but to reduce the number of possible branches of the solution, you need to choose a figure that can be in the smallest places on the current field. To do this, we take each type of figure and try on each place. When checking, we mark the used places of the field. If it turns out that there are places that cannot be covered, then the solution does not exist in this configuration - we reject the solution branch.
2. We put a piece in one of the possible places, thereby reducing the number of pieces and the size of the board. And recursively go to step 1.
Additional quick checks can be developed to pruning branches.
The choice of a place for the next figure can also be done not randomly, but according to some algorithm.
For the first example: 1x2 - 18 possible places, 1x3 - 11 places, 2x3 - 7 places. Therefore, we choose the third figure for the first branching step.
We put the first figure in the corner (0,0) vertically, we get the following picture:
0011
0011
0011
0100
When the first step of the algorithm is performed, it turns out that the field (1,3) cannot be covered with any figure - the branch breaks, go to the next option.
This algorithm will definitely find the right solution, since it reduces, in the worst case, to a complete enumeration.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question