Answer the question
In order to leave comments, you need to log in
State machine (identifier recognition) how to draw generic?
Hello. I can't solve the problem for days now:
Data:
<b> ::=A|B|C|...|Z (letter)
<c> ::=0|1|....|9 (number)
< identifier> ::= <b>
<identifier> ::= <iden-r><b>|<iden-r><c>
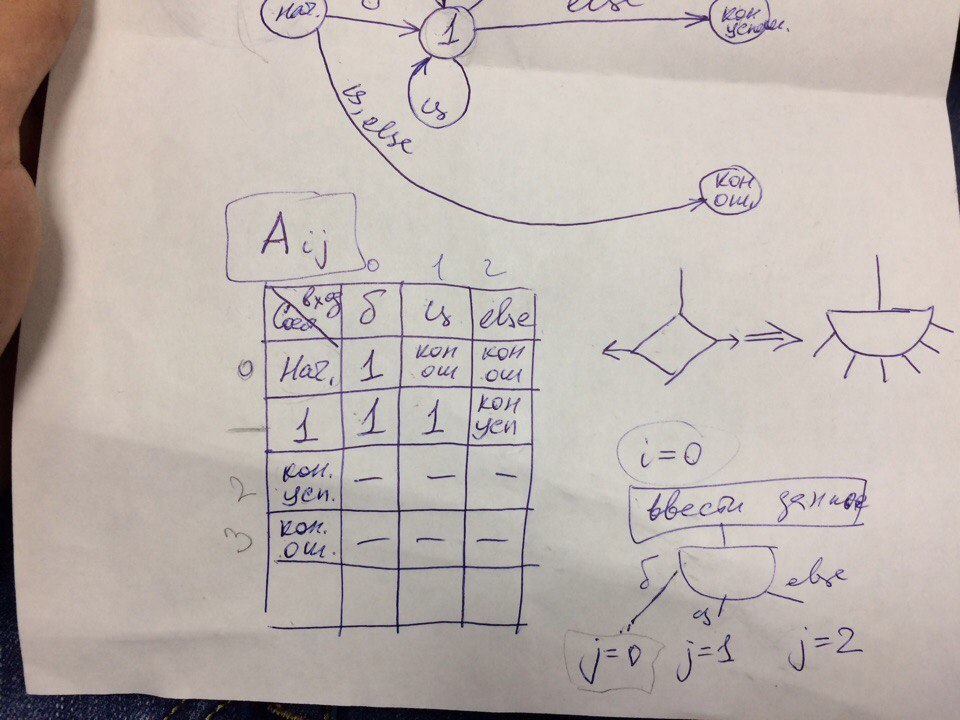
We have an initial state, there are two ways from it: when entering a letter, we get into the first state, and when you enter a number or something else (for example, a symbol), we get into the "Final erroneous" state. In the first state, we have paths: when we enter a letter or number, we return to the first state, and when we enter something else (else), we go to the "Final successful" state.
Roughly speaking, we have a state matrix and a drawn diagram of these transitions, and the task is to compile an algorithm for this finite state machine, with cycles, variables, and something else that I was told about. The algorithm must fit any finite state machine, that is, as I understand it, it cannot be customized to the descriptions in the task, because this algorithm must be universal for any number of rows and columns in the matrix, for example, the appearance of numbers with commas and any other additions.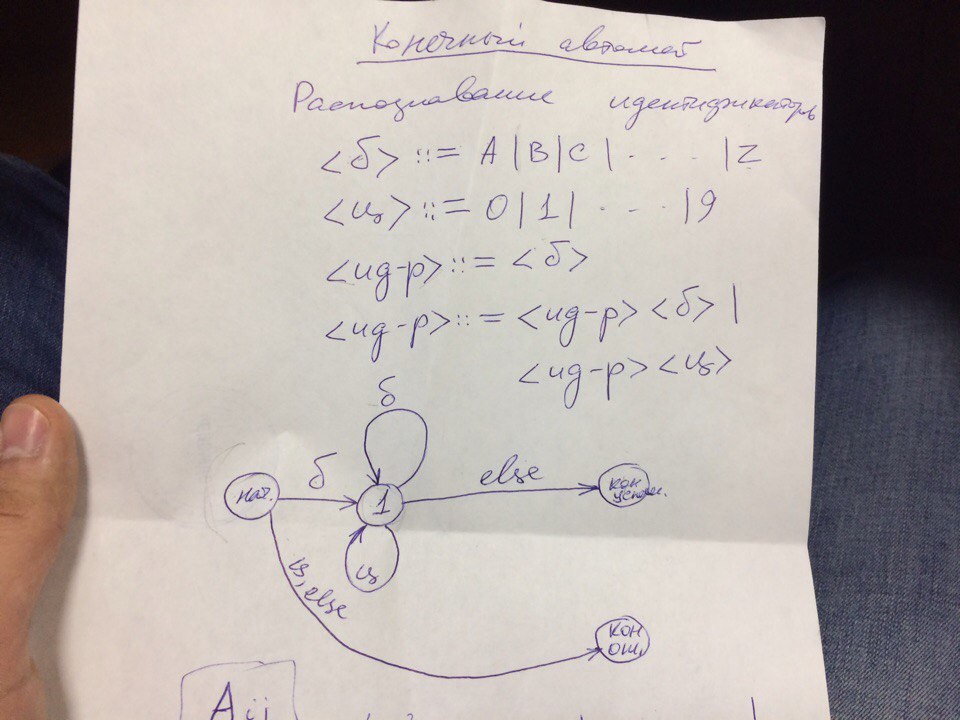
Answer the question
In order to leave comments, you need to log in
0. Set the initial state, set the pointer to the first character.
1. Get the next character.
2. Using the transition table, find the transition for the pair (state, symbol).
3. If there is such a transition, then set a new state, move the pointer to the next character, go to step 1.
4. Check the admissibility of termination in the current state using the admissibility table.
5. If the termination is invalid, then issue an error, exit.
6. Issue a correct termination, exit.
You have left recursion in your grammar. <identifier> ::= <id-r><b>|<id-r><c>
This cannot be implemented by a DFA. gotta get rid of her. Google "eliminate left recursion".
State machines are equivalent to regular expressions. But your assignment is written in terms of the Backus-Naur Form, which defines a context-free grammar. In general, grammars cannot be solved using DFA. But in your case it is very easy to write a regular expression: [AZ]([1-9]|[AZ])*. Kleene's theorem gives a way to construct an automaton that allows any regular expression.
You need to get an equivalent grammar first (generating the same language) suitable for building a state machine. Usually, an additional non-terminal is introduced for this.
Here you go to this man, look at
the problem
https://www.youtube.com/watch?v=XbihuriQ8p8&t=1h5m30s
solution
https://www.youtube.com/watch?v=wH4l8WvGPFE&t=1m20s
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question