Answer the question
In order to leave comments, you need to log in
Solution of the integral. How to find an error in a variable substitution?
There is an error in solving the integral: the answer does not converge with the solution in a different way and a banal check through mathematical packages.
Until the very last change to the variable v, everything is OK, and after solving the integral over dv, the answer is wrong with Log[(4/7)(2+x+x^2)] instead of Log[(2+x+x^2)] . I've been coming back to it for a week now and I'm probably slowing down a lot.
F=\frac{5}{2} \int \frac{x}{x^2+x+2} \, dx=\frac{(5\ 4) \int \frac{x}{\frac{4}{7} \left(x+\frac{1}{2}\right)^2+1} \, dx}{2\ 7}\left\{u=\frac{2 \left(x+\frac{1}{2}\right)}{\sqrt{7}};du=\frac{2 dx}{\sqrt{7}};x=\frac{\sqrt{7} u}{2}-\frac{1}{2};\right\}F=\frac{\left(5\ 4 \sqrt{7}\right) \int \frac{\frac{\sqrt{7} u}{2}-\frac{1}{2}}{u^2+1} \, du}{2\ 7\ 2}=\frac{5 \int \frac{\sqrt{7} u-1}{u^2+1} \, du}{\sqrt{7} 2}=\frac{5}{2} \int \frac{u}{u^2+1} \, du-\frac{5 \int \frac{1}{u^2+1} \, du}{\sqrt{7} 2}=\frac{5}{2} \int \frac{u}{u^2+1} \, du-\frac{5 (2 x+1)}{\left(2 \sqrt{7}\right) \left(\sqrt{7} \tan \right)}\left\{v=u^2+1;dv=2 u du;\right\}F=\frac{5}{4} \int \frac{1}{v} \, dv-\frac{5 (2 x+1)}{\left(2 \sqrt{7}\right) \left(\sqrt{7} \tan \right)}=\frac{5 (v \log )}{4}-\frac{5 (2 x+1)}{\left(2 \sqrt{7}\right) \left(\sqrt{7} \tan \right)}=\frac{5}{4} \left(\left(\left(\frac{2 \left(x+\frac{1}{2}\right)}{\sqrt{7}}\right)^2+1\right) \log \right)-\frac{5 (2 x+1)}{\left(2 \sqrt{7}\right) \left(\sqrt{7} \tan \right)}=\frac{5 \left(\left(4 x^2+4 x+8\right) \log \right)}{4\ 7}-\frac{5 (2 x+1)}{\left(2 \sqrt{7}\right) \left(\sqrt{7} \tan \right)}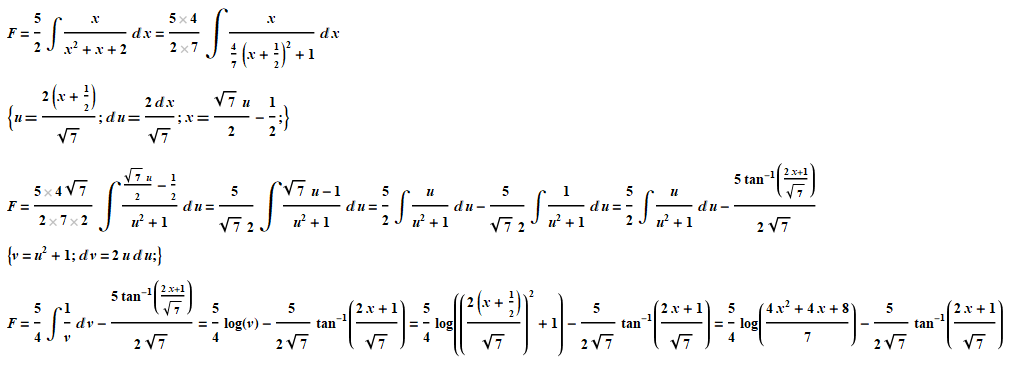
Answer the question
In order to leave comments, you need to log in
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question