Relationship between maximum flow search and Kruskal-Prim algorithm (too much code)?

B

BadCats2019-10-31 23:47:53

Algorithms

BadCats, 2019-10-31 23:47:53

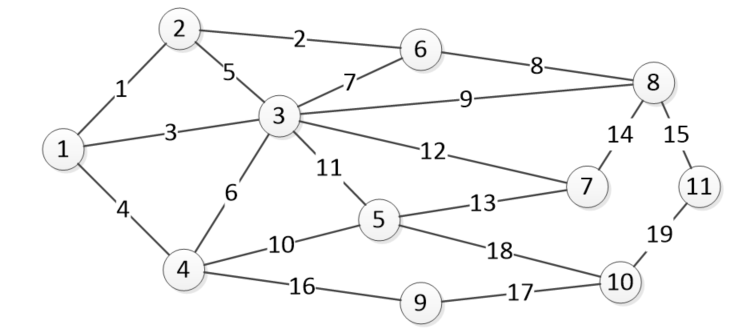
I wrote a small program to find the minimum spanning tree and (separately) the path with the maximum bandwidth:

the code

// Lab_6.cpp : Этот файл содержит функцию "main". Здесь начинается и заканчивается выполнение программы.
//

#include <iostream>
#include <vector>
#include <cstring>
#pragma warning(disable : 4996)
using namespace std;

int main()
{
  char data[] = "1-3-6,4-3-2,2-1-4-6-7-8-5,3-1-5-9,4-10-7-3,2-8-3,5-3-8,7-11-3-6,10-4,9-5-11,10-8"; //переставлена местами 1 и 2 вершины - соответсвенно варианту - путь 2-11
  char weight[] = "4-21-7,14-7-4,21-7-21-15-11-9-8,21-14-4-9,4-6-13-8,7-8-15,13-11-13,13-21-9-8,26-9,26-6-15,15-21";//переставлена местами веса для 1 и 2 вершин - соответсвенно варианту - путь 2-11
  char width[] = "2-20-5,3-4-2,20-4-20-9-8-8,20-3-3-4,3-3-7-8,5-3-4,7-4-3,5-20-8-3,8-4,8-3-9,9-20";//переставлена местами значений пропускной способности для 1 и 2 вершин - соответсвенно варианту - путь 2-11
  vector<string> lists;
  vector<vector<int>> weight_vec;
  vector<vector<int>> width_vec;
  vector<vector<int>> vertices;
  //парсинг строки
  //парсинг вершин
  char* pch = strtok(data, ","); // во втором параметре указаны разделитель (пробел, запятая, точка, тире)
  while (pch != NULL)                         // пока есть лексемы
  {
    //std::cout << pch << endl;
    lists.push_back(pch);
    pch = strtok(NULL, ",");
  }
  for (auto& i : lists)
  {
    pch = strtok(const_cast<char*>(i.c_str()), "-");
    vector<int> sub_v; // подсписки вершин, разделенные запятой
    while (pch != NULL)                         // пока есть лексемы
    {
      sub_v.push_back(atoi(pch));
      pch = strtok(NULL, "-");
    }
    vertices.push_back(sub_v);// формируем вектор списков вершин
  }
  //конец парсинга вершин
  lists.clear();
  //парсинг массива весов
  pch = strtok(weight, ","); // во втором параметре указаны разделитель (пробел, запятая, точка, тире)
  while (pch != NULL)                         // пока есть лексемы
  {
    //std::cout << pch << endl;
    lists.push_back(pch);
    pch = strtok(NULL, ",");
  }
  for (auto& i : lists)
  {
    pch = strtok(const_cast<char*>(i.c_str()), "-");
    vector<int> sub_v; // подсписки вершин, разделенные запятой
    while (pch != NULL)                         // пока есть лексемы
    {
      sub_v.push_back(atoi(pch));
      pch = strtok(NULL, "-");
    }
    weight_vec.push_back(sub_v);// формируем вектор списков вершин
  }
  lists.clear();
  //Парсинг пропускной способности потоков
  pch = strtok(width, ","); // во втором параметре указаны разделитель (пробел, запятая, точка, тире)
  while (pch != NULL)                         // пока есть лексемы
  {
    //std::cout << pch << endl;
    lists.push_back(pch);
    pch = strtok(NULL, ",");
  }
  for (auto& i : lists)
  {
    pch = strtok(const_cast<char*>(i.c_str()), "-");
    vector<int> sub_v; // подсписки вершин, разделенные запятой
    while (pch != NULL)                         // пока есть лексемы
    {
      sub_v.push_back(atoi(pch));
      pch = strtok(NULL, "-");
    }
    width_vec.push_back(sub_v);// формируем вектор списков вершин
  }
  //конец парсинга

  //сортировка весов
  for (size_t i = 0; i < weight_vec.size(); i++)
  {
    for (size_t j = 0; j < weight_vec[i].size(); j++)
    {
      for (size_t k = 0; k < weight_vec[i].size(); k++)
      {
        if (weight_vec[i][j] < weight_vec[i][k])
        {
          swap(weight_vec[i][j], weight_vec[i][k]);
          swap(vertices[i][j], vertices[i][k]);
        }
        
      }
    }
  }


  // сортировка пропускной способности
  /*for (size_t i = 0; i < width_vec.size(); i++)
  {
    for (size_t j = 0; j < width_vec[i].size(); j++)
    {
      for (size_t k = 0; k < width_vec[i].size(); k++)
      {
        if (width_vec[i][j] > width_vec[i][k])
        {
          swap(width_vec[i][j], width_vec[i][k]);
          swap(vertices[i][j], vertices[i][k]);
        }

      }
    }
  }*/



  int countt = 1;
  //отобранные веса
  /*cout << "sorted weights " << endl << endl;
  for (auto& i : weight_vec)
  {
    cout << "vertices " << countt << endl << "--------------------" << endl;
    for (auto& j : i)
    {
      cout << j << endl;
    }
    cout << endl << "--------------------" << endl;
    countt++;
  }*/

  //долбанное остовное дерево
  for (size_t i = 0; i < vertices.size(); i++)
  {
    for (size_t j = 0; j < vertices[i].size(); j++)
    {
      int index = 0;
      if (vertices[i][j] > 0)
      {
        index = vertices[i][j] - 1; // индексом становится значение из ячейки вектора (-1 -т.к нумерация с 0)
      }
      else if (j < vertices[i].size() - 1 && vertices[i][j + 1] > 0) //если уже "затерли" вершину - проверяем - мржем ли перейти к следующей
        // и не "затерта" ли она
      {
        index = vertices[i][j + 1] - 1;
      }
      else
      {
        index++; //если значения в векторе затерты - просто "вручную" двигаемся дальше - не перепрыгивая по значению
      }
      int border = 0; // граница цикла для разной длины под-векторов - что бы не выйти за пределы меньшего вектора
      bool flag = false;
      //определяем, какой из двух векторов более короткий и размер которого станет границей для цикла
      if (vertices[index].size() > vertices[i].size())
      {
        border = vertices[i].size();
      }
      else
      {
        border = vertices[index].size();
        flag = true;//переменная, показывающая, длина которого из векторов стала границей массива (необходимо для дополнительного прохода)
      }
      for (size_t k = 0; k < border; k++)
      {
        for (size_t t = 0; t < border; t++)
        {
          if (vertices[index][k] == vertices[i][t] /*|| vertices[index][k] == j + 1*/)
            // если мы перешли в указанный индекс и там в списке вершин нашли такую же, 
            //как в том списке ИЗ которого мы перешлы - образуется петля - две разные вершины - указывают на одну
          {
            vertices[index][k] = -1;// затираем эту вершину, в том списке В который перешли - разрываем петлю
            /*vertices[i][k] = -1*/;// затираем эту вершину, в том списке ИЗ которого перешли - разрываем петлю
            vertices[i][j] = -1;// затиреам упоминание о соседней вершине - как о "соседней" в текущей вершине, образовывашей петлю

          }
          //дополнительный проход - для суб-векторов разной длины, если одинаковый элемент находится в конце более длинного вектора
          if (flag)
          {
            int delta = vertices[i].size() - vertices[index].size();
            for (size_t d = 0; d < delta; d++)
            {
              if (vertices[index][k] == vertices[i][t + d] /*|| vertices[index][k] == j + 1*/)
              {
                vertices[index][k] = -1;
                //cout << "OK" << endl;
              }
            }
          }
          else
          {
            int delta = vertices[index].size() - vertices[i].size();
            for (size_t d = 0; d < delta; d++)
            {
              if (vertices[index][k + d] == vertices[i][t] /*|| vertices[index][k] == j + 1*/)
              {
                vertices[index][k] = -1;
                //cout << "OK2" << endl;
              }
            }
          }
          //конец дополнительного прохода
        }
      }
    }
  }
  int cnt = 1;
  //отобранные вершины
  cout << "selected vertexes" << endl << endl;
  for (auto& i : vertices)
  {
    cout << "vertices " << cnt << endl << "--------------------" << endl;
    for (auto& j : i)
    {
      cout << j << endl;
    }
    cout << endl << "--------------------" << endl;
    cnt++;
  }

}

separately sorting by weight, separately by throughput - I comment on one of them.
I get the following results:
Source graph:

(no need to look at the weight indicated in the image - by condition, another one is given.)

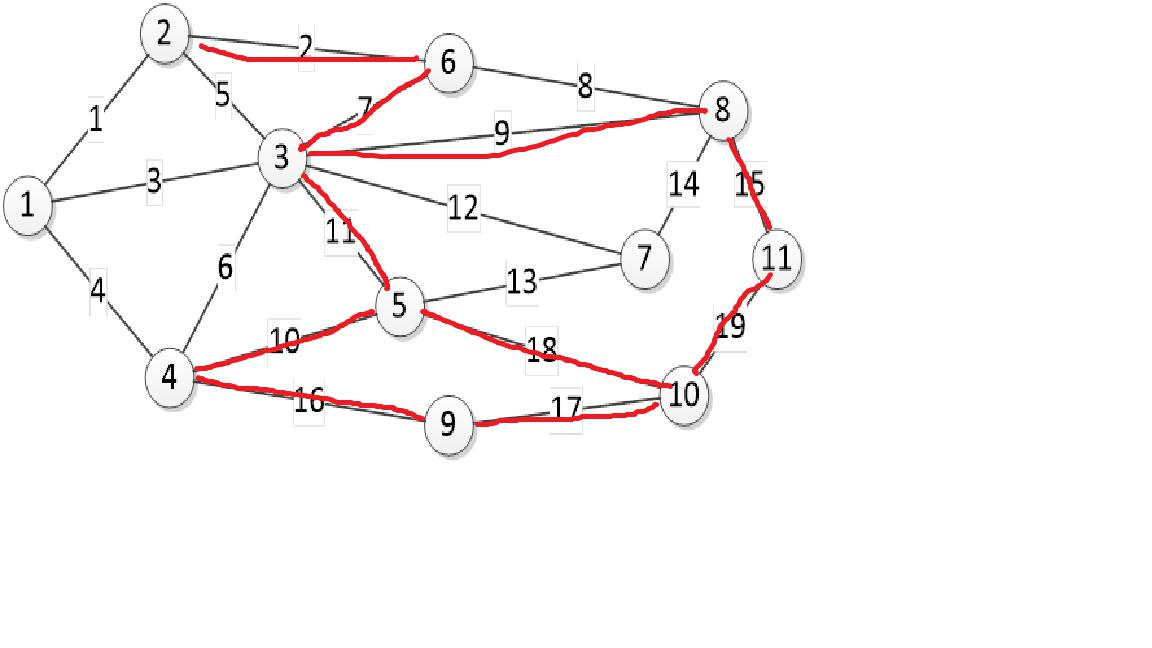- a case for finding the maximum flow.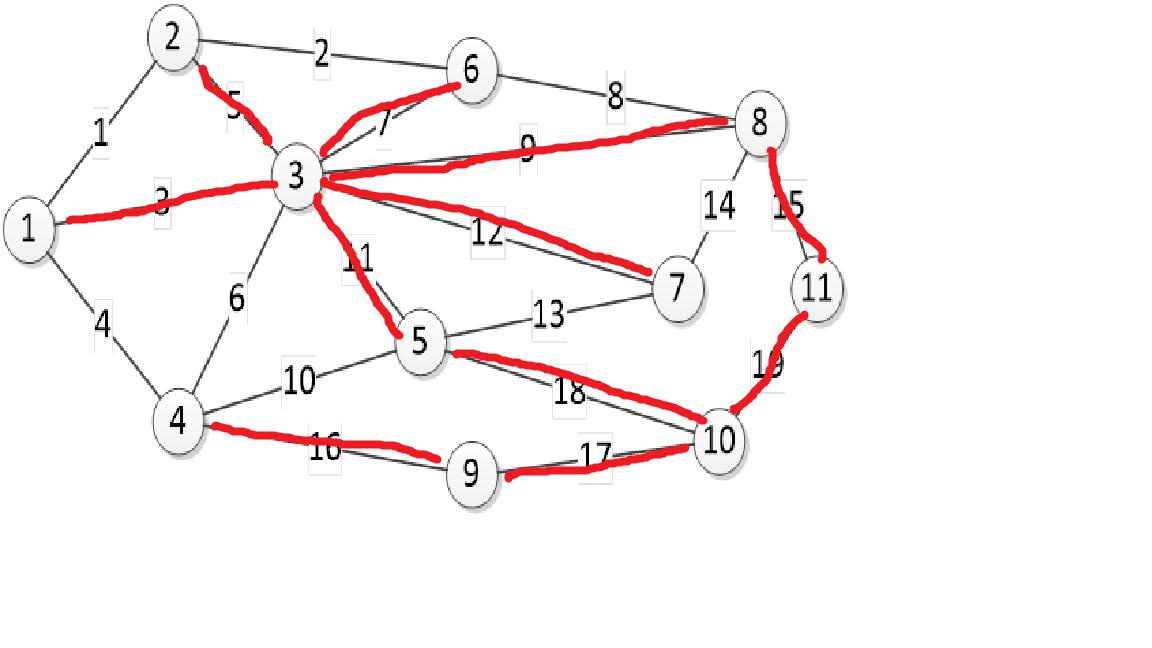

is the minimum spanning tree.
Actually, the question itself is:
Why, when sorting by bandwidth, this condition is "violated":

if (vertices[index][k] == vertices[i][t] /*|| vertices[index][k] == j + 1*/)
            // если мы перешли в указанный индекс и там в списке вершин нашли такую же, 
            //как в том списке ИЗ которого мы перешлы - образуется петля - две разные вершины - указывают на одну
          {
            vertices[index][k] = -1;// затираем эту вершину, в том списке В который перешли - разрываем петлю
            /*vertices[i][k] = -1*/;// затираем эту вершину, в том списке ИЗ которого перешли - разрываем петлю
            vertices[i][j] = -1;// затиреам упоминание о соседней вершине - как о "соседней" в текущей вершине, образовывашей петлю

          }

- forbidding to form loops? -i.e., in the case of minimum weight - for example, for vertices 5-4-9-10 - even though vertex 5 and 9 point to 10, a complete - closed loop is not formed - as I understand it, due to the sorting properties - i.e. properties of finding the minimum weight by definition? But, when using the same sorting method (elementary bubble), but with a different rule - by capacity - transition over vertices by definition - it happens in such a way that a loop is formed (and this is correct, in theory - the flows merge) (vertices 5-4 -9-10), but is there a pattern in this, is such a feature - a property of a graph / graphs - by its nature?
That is, once again, the question is more concise:Why, under the same graph traversal condition, but in a different order (priority) - different results are obtained, one of which contradicts the original traversal condition?