Recurrent formula precision?

Question

C++ / C#

It is necessary to calculate the function using the recursive ratio of the terms of the series.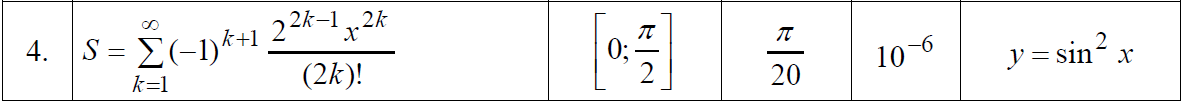

Here is my recursive formula:

Program code:

#include <cmath>
#include <iostream>
#include <conio.h>
using namespace std;

int main() {
  const double pi = 3.14159265358979323846;
  double x = pi / 2;
  double s = 0,
    eps = 1e-06;
  int k = 1;
  double elem = x * x;
  s = elem;
  while(fabs(elem) >= eps) {
    cout << k << " : " << elem << " : " << s << endl;
    ++k;
    elem *= (-4 * x * x) / ((2 * k + 1) * (2 * k + 2));
    s += elem;
  }
  cout << "S: " << s << endl;
  cout << "MATH: " << sin(x) * sin(x);
  _getch();
    return 0;
}

Actually, the problem is that the result of my formula is wildly different from the result of functions from the library. There are suspicions that the formula is not correct, but rewrote it several times.

Answer 1

You have derived the formula for getting k+1 element from k-th, and in the program you use it to get k-th element from k-1. These are different formulas.

Answer 2

It's just that the ratio is correct. Next, you need to choose the correct initial values ​​and the correct check to stop.