Answer the question
In order to leave comments, you need to log in
Procedural generation of a random world from 100 by 100 cells?
I studied the Voronov algorithm, as soon as I understood it, I realized that it would not suit my task (since the map itself (due to its small size) is already a particular solution with square polygons).
The task is to generate a continent of 100 by 100 cells, and distribute its territory into N countries with random sizes. That is, I don’t understand how to group neighboring cells in an area without different enclaves.
I can't find anything suitable.
Here is an example, that is, there is a partition, but I can’t understand how to group at all. And to find, all articles end with the construction of a Voronov diagram, and I can’t catch up with what to do next.
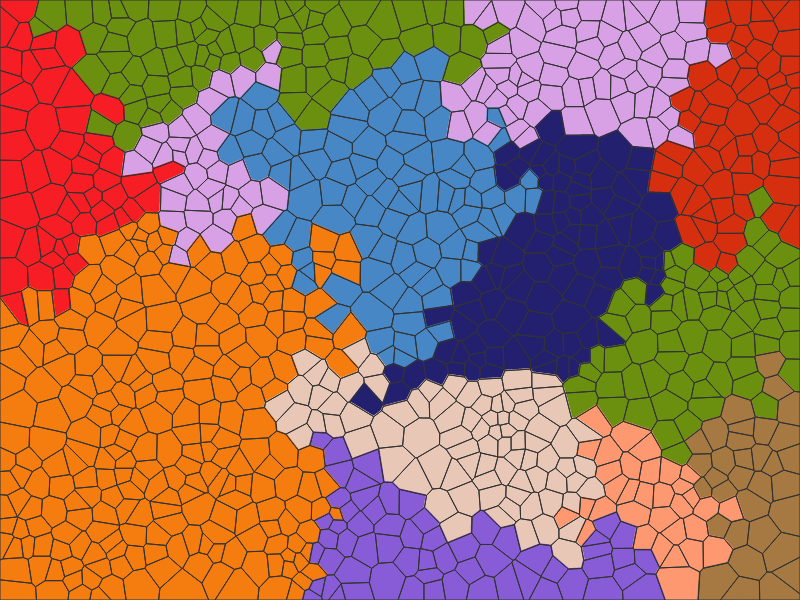
Answer the question
In order to leave comments, you need to log in
Intuitively, you can act like this:
1. Drop different paints at N randomly selected starting points.
2. Choose a color for painting the next point (randomly or sequentially).
3. Find a point of the selected color that has not been worked with yet (you need to exit the loop if all the points have been worked out).
3.1. If there are no unpainted neighbors, then remember that we worked with this point, go again to step 3 (or step 2, you can choose randomly).
4. Choose an uncolored neighbor near this point (randomly).
5. Paint the neighbor with the chosen color.
6. Remember that you worked with the point selected in step 3. Go to step 2.
7. The points you didn't work with ran out - most likely it's time to display the result.
Here is a simplified version of "on the fingers":
import cv2
import numpy as np
from PIL import Image
from itertools import product
N = 42
W = 200
H = 200
def distance(p1, p2):
y1, x1 = p1
y2, x2 = p2
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
canvas = np.zeros((H, W, 3), dtype=np.uint8)
centers = np.unravel_index(np.random.randint(0, W * H, N), canvas.shape[:2])
canvas[centers] = np.random.randint(0, 256, (N, 3))
centers = list(zip(*centers))
for x in range(0, W):
for y in range(0, H):
cy, cx = min(centers, key=lambda center: distance(center, (y, x)))
canvas[y, x] = canvas[cy, cx]
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question