Problem with YAC, how?

Question

Counts

Many of the habravchans were at the Yandex YAC2011 conference. Many of those who were there saw the Yandex school site and probably tried to solve puzzles. I tried too. And I tried for a very long time. I did not find a solution that would satisfy the representatives of the Yandex school, so I decided to turn to the habra community for help.
The task sounds like this: " Give an example of a graph in which the degrees of all vertices are equal to 3, but it is impossible to split the vertices into pairs of adjacent ones ."
I made my first decision in about 5 minutes. It looked like this: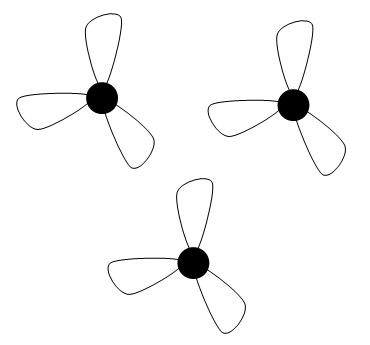

Of course, one vertex could have been enough instead of three, but then I didn’t think about it.
Strangely, they told me that my decision was wrong. Moreover, I was told that what I drew was not a graph. I sat there for about an hour, trying to solve this problem, so I didn’t think of anything, and went to work.
Arriving home, I reached into my textbooks. It turns out that a graph is a triple Г=(X,U,Ф), where X is a finite set of vertices; U is a finite set of arcs; Φ is a three-place incidence relation Φ(x,u,y), where x,y are elements of the set X, u is an element of the set U. In addition, two conditions are imposed on Φ: 1. An edge always connects a pair of vertices; 2. An edge corresponds to at most one pair of vertices.
My question is this:
1. Is my decision really wrong?
2. If it is wrong, what does the correct solution look like?

Answer 1

Correct answer: "fan" with "envelopes" on the blades.
The "envelope" looks like this: "Fan": We hook the upper top of the "envelope" to the blades of the "fan". Total: 5 * 3 + 1 top. Odd cannot be, since pairs are needed. On Yak, this solution was credited, but they said that it was possible if with a smaller number of vertices.

*
/\
*-*
|X|
*-*


|
*
/\


Answer 2

Well, the degree of the vertices on your graph is 6.

Answer 3

In short, we need to find a complete bipartite cubic homogeneous/regular graph

Answer 4

An interesting problem. I have not found a solution yet, but the fact that your version is incorrect can be judged from the description of the degree of the vertex:
“The degree of the vertex of a graph is the number of edges emerging from it. In this case, it is considered that the loop
exits the vertex twice.
In your graph, the degree of the vertices is 6

Answer 5

A three-blade fan with loops at the top?

Answer 6

And what does it mean "you cannot split vertices into pairs of adjacent ones"? Odd number of vertices?

Answer 7

Still, I didn’t understand what it means to “split the vertices into pairs of adjacent ones” ...
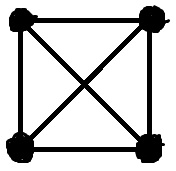
Would such a graph be a solution?

Answer 8

Googled: Discrete Mathematics. Part 3 (Course of lectures). Authors: Yemtseva E.D., Solodukhin K.S.
On page 1 , the definitions of a graph are introduced, if repeating edges are allowed - a multigraph, if loops are allowed - a pseudograph.
It seems that a graph further in the text is understood as one in which there are no repeating edges and loops. To be honest, this moment is not very understood.
Further, on page 4 , the definition of the degree of a vertex and an interesting theorem are given: In any homogeneous graph, either its order or its degree is an even number (homogeneous - the degrees of all its vertices are equal). Those. just our case. We have that in our case, the graph must definitely have an even number of vertices (this is to the comment above ).

Answer 9

Yes, I got too carried away with drawing. The rib really needs to be removed.