Pathfinding algorithm?

Question

Algorithms

Hello.
There is such a game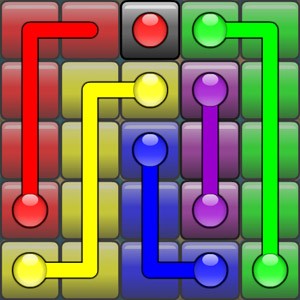

The goal is to connect the same colors without leaving empty cells.
It became interesting to me how it is possible to implement the generation and solution of such levels.
I have absolutely no idea where to dig. Please tell me what to google.

Answer 1

If the level plans are exactly the same in content as the picture shown (i.e. connected, do not contain diagonal turns and there are no other hidden conditions), then the pathfinding algorithm:
1) poke at a random point, its color is yellow, add it to area Yellow1
2) look for a yellow point in the vicinity, if 1 or 2 new points are found (not yet recorded in Yellow) - then repeat the cycle with them, look for the next surrounding points
3) stop searching for Yellow when both ends of the Yellow area are reached
4) poke a new random point, its color is Red - repeat from 1)
5) when all the cells of the field are in the sets Yellow1, Yellow2, Red1, etc. - stop.
You can also read abouten.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC_%D0%BF%D0%BE%D0 %B8%D1%81%D0%BA%D0%B0_A * and other pathfinding algorithms
en.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B8%D1%81%D0%BA_%D0 %BF%D1%83%D1%82%D0%B8
Level generation - take a random color Blue, randomly determine its first point, add it to Blue1, then randomly determine the step - horizontally or vertically, add each new Blue point to Blue1 + into used, at each step we randomly decide whether to complete the color Blue or go to Red. Repeat until the entire field is used. We get a similar level.

Answer 2

You can not select connectivity components, but simply assume that there are no transitions between cells of different colors. In this graph, construct a Hamiltonian cycle for each connected component.
You can read more here: e-maxx.ru/algo/
All of the above makes sense if you know what a graph, adjacency table, etc. are. If not, give me a beacon. I will write in more detail.

Answer 3

Finding a solution:
For classical depth / breadth walks, we need to think of this problem as "getting from A to B". To do this, I propose to consider the following solution:
1. Let's number the colors. Let it be 1 - Blue, 2 - Yellow ... 5 - Green.
2. For each color, select a "start point" and a "finish point".
3. Now for point A we take the beginning of the 1st color, for point B we take the finish of the last.
4. Let's agree that a move can be made from the cell according to the following rules:
* From the start point, a move is made only to empty points or to the finish point of the same color.
* From a regular point, a move is made only to empty points or to a finish point of the same color.
* From the Finish we "teleport" to the starting point of the next color.
* If we have reached point B (and bypassed all the points of the field), then the bypass is over, the solution has been found.
5. At each step, paint the point with the current color.
6. Traverse the resulting graph in depth or width using classical methods (I would do a recursive depth traversal).
Option 1 - put points randomly and look for a solution. Found a solution? Here is the new card.
Option 2 - go around the entire field with 1 line with random turns. At the start point - the beginning of the 1st color. At the end point - the finish of the last color. We select 4 places (to get 5 segments) on this line (with a distance between them of at least 2 cells), put 2 markers in the selected places: the end of the previous color (bypass) and the beginning of the next.
What to google: graph theory, pathfinding algorithms.
PS who wants to play - the keywords to search for "Flow".