Linear regression equation. "The proportion of variance explained by the influence of the independent variable." How to understand?

Question

Regression analysis

Hello! There was a problem with understanding the concept of explained variance. For example, we want to calculate the coefficient of determination for our linear regression model. It is clear that the proportion of explained variance + the proportion of random = 1 and from this it follows that the proportion of explained variance = 1 - the proportion of random variance. However, in the resource on which I study this topic, the proportion of random variance is expressed as the sum of the squared deviations of the original values ​​​​of the dependent variable from the regression line. But these deviations can be caused by both the independent variable and other factors! Why, then, deviations from the regression line considered to be caused by unaccounted for factors? Thanks for answers!

Answer 1

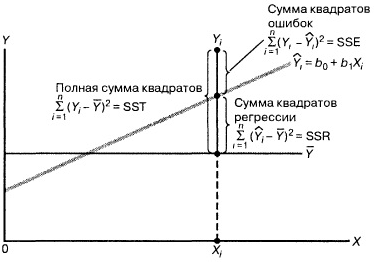
Let's look at the picture. Everything should be clear from it, from what and how errors are added. What is called the "sum of squares of error" in the figure would, of course, be better called "the sum of squares of the error that is not explained by the resulting regression equation."
It may seem a little unexpected, except that squares appear in the figure. But the ratio - the total sum of squares is equal to the sum of two sums of squares - is proved in any "decent" resource.