Answer the question
In order to leave comments, you need to log in
How to write the sum formula?
Good afternoon! Can you please tell me how to write number B?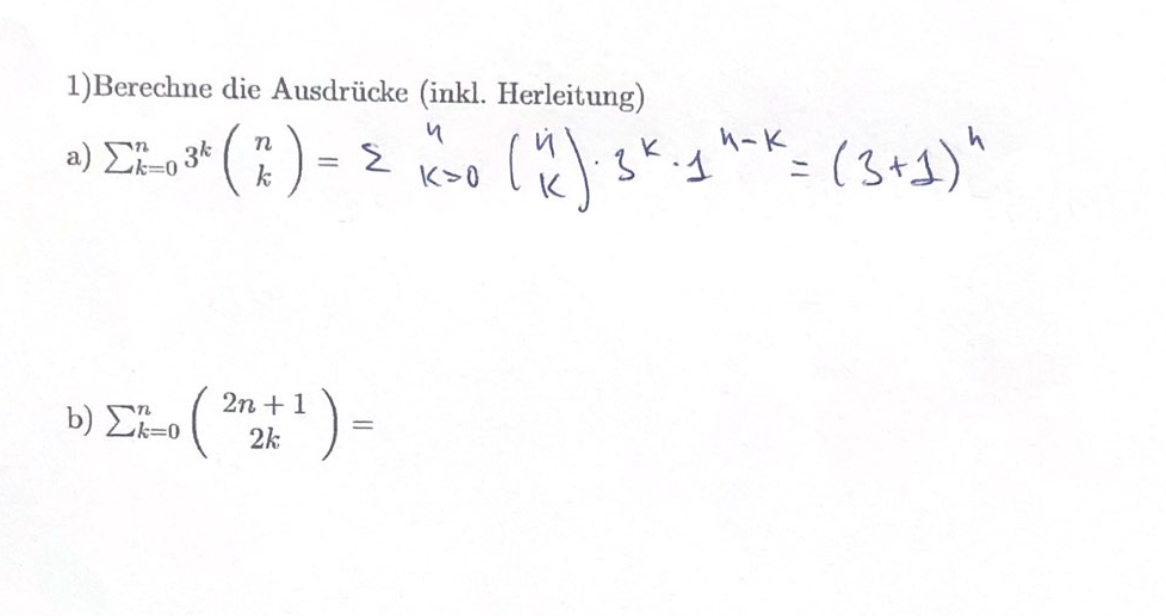
Answer the question
In order to leave comments, you need to log in
In my notation C (n, k) - combinations of n by k.
You need to know this identity for combinations:
С(n,k) = C(n,nk).
Applying to what we have under the sum sign:
C (2n + 1, 2k) \u003d C (2n + 1, 2n + 1-2k)
When k goes from 0 to n, combinations are obtained on the left for all even numbers from 0 to 2n+1, and on the right - over all odd ones.
There is a formula that the sum of all combinations of n over all possible k will be 2 ^ n, It turns out stupidly from the disclosure of (1 + 1) ^ n by Newton's binomial.
But we do not have a sum for all, but only for even ones. But we have already seen above that the sums over all even and all odd coincide. This begs the variant to simply calculate the doubled required amount.
Formally: let X be the required sum in the problem.
then
X+X = sum_{k=0..n} C(2n+1, 2k) + sum_{k=0..n}(2n+1, 2n+1-2k) =
= sum_{k=0. .n} C(2n+1, 2k) + sum_{k=0..n}(2n+1, 2*(nk)+1) =
= sum_{k=0..n} C(2n+1 , 2k) + sum_{k=n..0}(2n+1, 2*(nk)+1) =
Replace nk=j in the second sum. Because k=n..0, then j = 0..n.
= sum_{k=0..n} C(2n+1, 2k) + sum_{j=0..n}(2n+1, 2*j+1).
And this is a stupid sum over all possible k from 0 to 2n+1 (only even and odd in separate sums):
= sum_{k=0..2n+1} C(2n+1, k) = 2^(2n+ 1)
Ostuda X = 2^(2n+1) / 2 = 2^(2n)
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question