How to tile an axis-oriented Rectangle with blocks of the maximum size, bypassing obstacles?

Question

Algorithms

Good day.
The task of finding a path and the ability to attack (the absence of obstacles in a given direction at the right distance) - we need to optimize the construction of a conditional Navigation mesh .
There is a large ready-made cross-country grid (there are up to 1000x1000), divided into "8x8 squares" with impassable sectors (red in the pictures).
By combining traversable sectors (1x1) inside "8x8 squares" I build navmesh faces whose centers I use as graph nodes.
A simple solution that works now is splitting the "8x8 square" into 1xN strips,

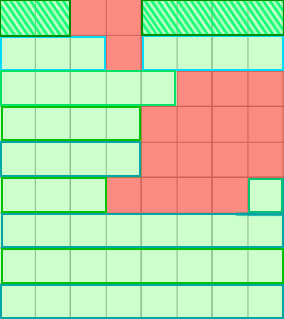
but this is a bit slow - I would like to speed it up by 2-4 times.

It will most likely work just fine like this:

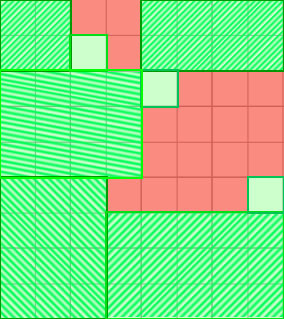
Tell me an algorithm (maybe there is some ready-made mathematical implementation) that can be used to get passable sectors of the maximum size

Answer 1

Firstly, it is not very clear why you do this at all. Aggregating squares into rectangles, you will find not the shortest paths in this graph. What algorithm do you work with next in the graph? Some Jump point search on non-aggregated cells can be faster than anything on aggregated ones.
Further, if you so desire, then your aggregation problem is NP and, apart from exhaustive enumeration, you will not find the optimal solution. But you seem to be getting some reasonably good solution, not just the optimal one. Then all sorts of greed and heuristics will work. It is possible, for example, to take the top-left-most uncovered cell and greedily grow around it the maximum area rectangle that does not intersect any covered or forbidden cell (for example, by going over the lower and upper boundaries and greedily inflating the left and right to the maximum). Using the example from the question, this algorithm will build 7 rectangles.

Answer 2

A simple solution that works now is to split the "8x8 square" into 1xN strips,

I will offer an easily implemented improvement, although it does NOT guarantee optimality.
Take your finished 1xN strips. If a strip with the same start and end coordinates adjoins this strip from below or above, then merge these strips. You continue the check, if the same strip adjoins the received block, then we attach it to the block, etc.
The advantage is simplicity.
In your example, this will give 8 blocks instead of 12 stripes.

Answer 3

In your example, this will give 8 blocks instead of 12 stripes.

Yes, ATP, so it will turn out 7 strips and 2 blocks. 
There is also an option to additionally generate to the same "8x8 square" according to the same scheme, but on vertical stripes, and choose the best one. 
How much will be the gain from such optimization - it is necessary to check.
Squares without obstacles inside me are not cut into strips anyway and are taken as 8x8