How to split numbers into groups so that the groups contain numbers that are close in value?

Question

Mathematics

Greetings.

There are many numbers and it is necessary to divide them into groups that are close in meaning to the numbers.
I can't think of a grouping algorithm. Suggest options.

Example (we divide the list into three groups):

[исходные числа] >>> [разбитые по группам числа]

[1,2,3] >>> [1][2][3]
[1,2,3,4,5,6] >>> [1,2][3,4][5,6]
[10,30,60,90,150] >>> [10,30][60,90][150]
[10,30,30,35] >>> [10][30,30][35]
[1,50,250,350] >>> [1][50][250,350]
[1,2,3,500,550,650,650] >>> [1,2,3][500,550][650,650]

Numbers can be anything.

Answer 1

This is called clustering, and the most popular method for it is K-means.

Answer 2

We need to introduce some kind of metric - some kind of numerical evaluation that would tell you why is better than . For example, you can take the maximum difference of two numbers in any group. Or the sum of squared distances from all numbers to the average in their group. Or the minimum distance between numbers in different groups (this must be maximized).
Then you can apply one of the well-known clustering methods, depending on the selected metric. In the case of one dimension, as you have (just numbers), you can also apply dynamic programming. This method works for almost any sane metric. Consider the function F(n,k) - the best possible metric if the first n numbers are divided into k groups. To recalculate, it is necessary to sort out how many numbers go to the last group (i), and recalculate the metric based on F(ni, k-1). choose the best one from all options.

Answer 3

Example from MatLab (via binary trees) ( cluster analysis )

PD = pdist(Data);             % (Data,'cityblock');
Z = linkage(PD,'average');   % (PD);
dendrogram(Z)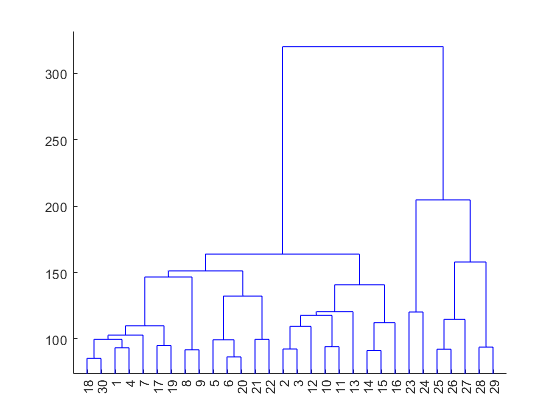

c = cophenet(Z,PD)
%I = inconsistent(Z);

T = cluster(Z,'cutoff',cut);
% или T = cluster(Z,'maxclust',nClust);