How to prove the equality of sets?

Question

Mathematics

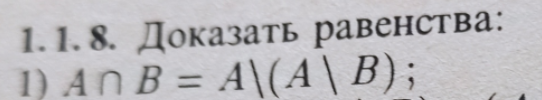
1) At the intersection of a and bx will belong to both the set a and the set b.
2) With the difference on the right side in the brackets, x will belong to a and will not belong to b. With another difference of the set a to the bracket x, a will belong and will not belong to a and will belong to b.
What is the problem? It seems to me that I do not understand the process of expanding the brackets on the right side

Answer 1

It is necessary to prove by the definition of equality of sets.

Answer 2

Formally, according to the laws of logic and definitions.
What does it mean that some element belongs to the right set?
x in A\(A\B), if and only if x in A AND x not in (A\B
) that (x in A AND x not in B). According to the laws of logic, this will be (x not in A OR x in B). add the first part to this and open the brackets:
x in A AND (x not in A OR x in B) = (x in A AND x not in A) OR (x in A AND x in B).
The first part is always false and cancels out, it remains only (x in A AND x in B), which by definition x in A and B. We used only equivalence everywhere and from the definition that the element belongs to the right set, we got the definition that the element belongs to left set. So these 2 sets are equal.