Answer the question
In order to leave comments, you need to log in
How to normalize stretched data with non-linear normalization?
Here is an example, there is such a sequence (1, 1, 3, 5, 90) How to scale it (0.1) BUT NOT LINEAR. I've read a ton of ways already. but there is no main thing, some z-signs, dispersion. But there is no definitive answer. (0,1)
If linearly normalized, then all 4 points will be ~0, and 90->1. And I need to somehow exponentially normalize, so that 3, 5 would be close to 0.4 0.5.
Is there at least one example of how to get something like (0, 0, 0.2, 0.4, 1) from (1, 1, 3, 5, 90)?
For example, this way, to find Z for this set it will be (- 0.54, 0.54, -0.48, -0.42, 2 ) what are these numbers, what has changed? What to do with them
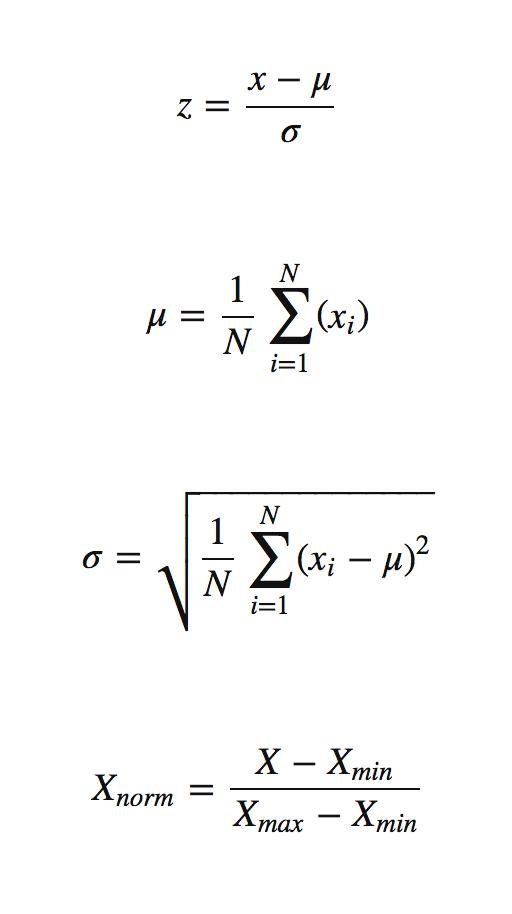
Answer the question
In order to leave comments, you need to log in
If you need to "increase small values", then you can use some convex function for each value, such as a cube root. Well, then, in the end, you still need a fourth formula in order to cram everything into the segment [0, 1]
Or even like this: first linearly normalize according to the fourth formula, and then apply some function F, increasing and convex on the segment [0, 1 ], such that F(0)=0, F(1)=1. For example a cube root.
Didn't find what you were looking for?
Ask your questionAsk a Question
731 491 924 answers to any question