How to make bots run away from pursuers?

Question

Algorithms

I have a large (non-tile) rectangular map bounded by outer polygons.
Inside it there are randomly generated raised polygons.
Conventionally, it looks something like this:


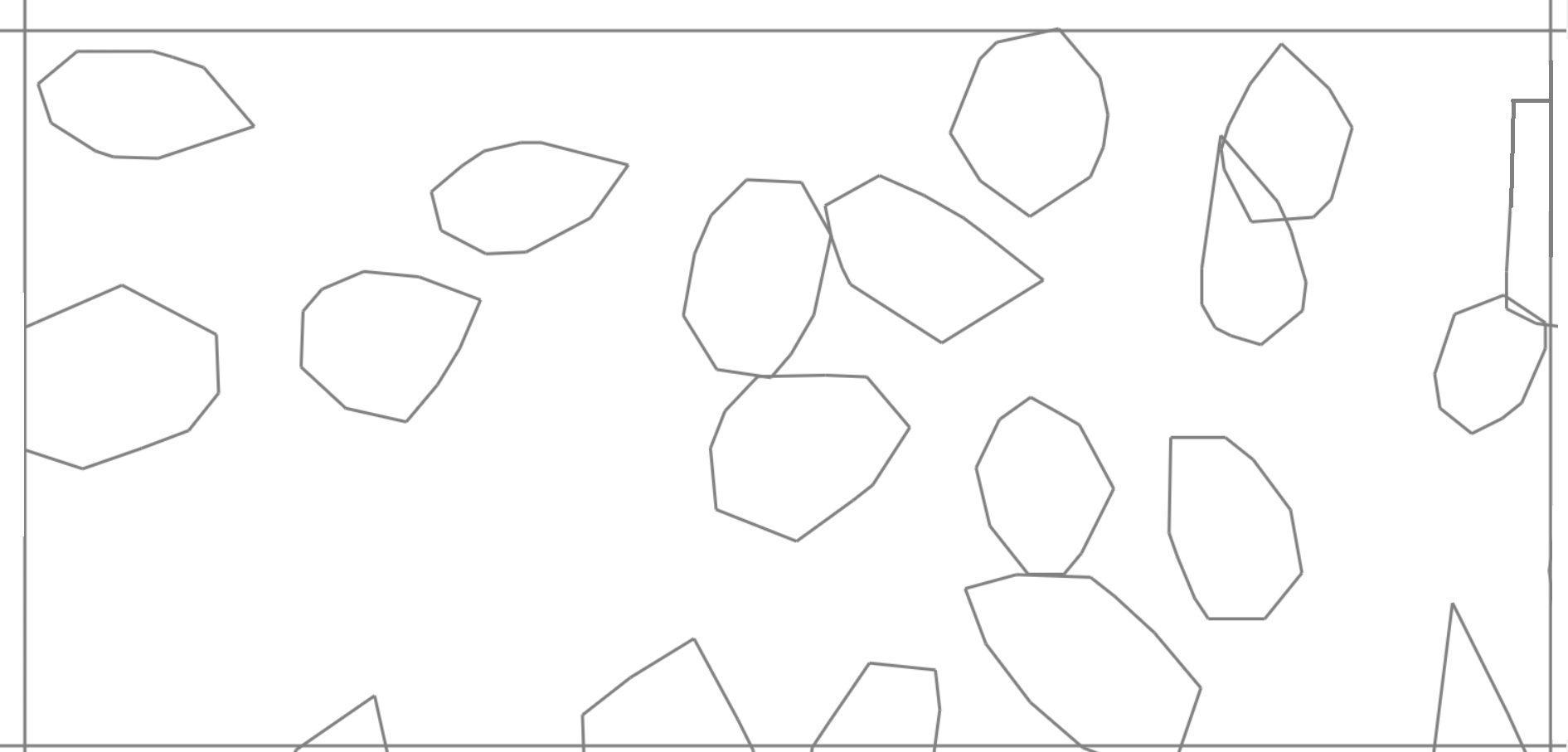
Some polygons can intersect, i.e. form a relatively long corridor with one exit.
Theoretically, the situation in the picture below is possible


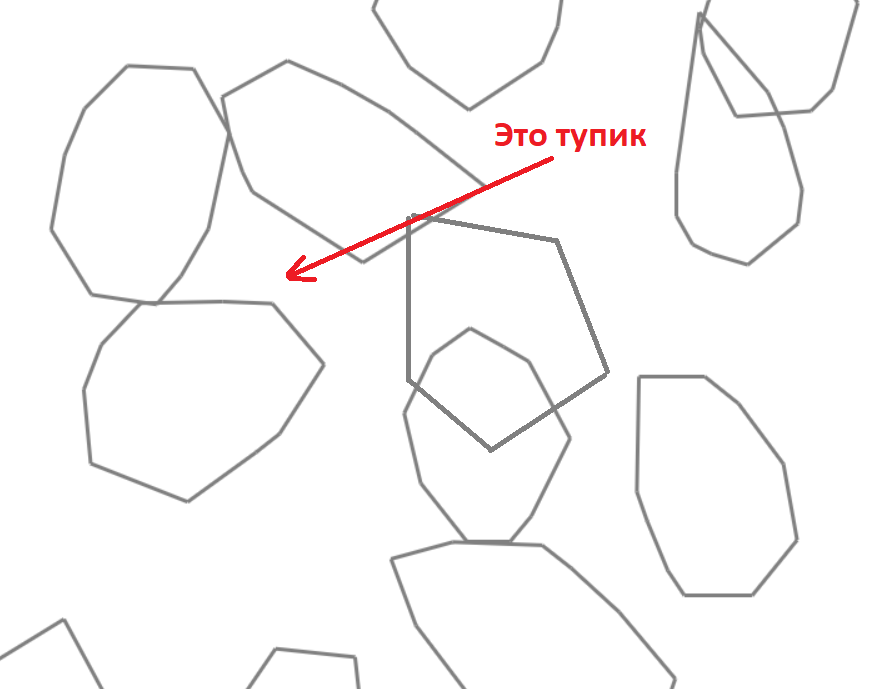
. Also, I have bots that can move to a certain point with avoiding obstacles, in an optimal way. Those. bots can chase someone, such as a player. (Let's call these bots red)

I need other bots (let's say green) that will run away from bots that can chase (from red). It is desirable that green bots know how to bypass dead ends. if they go there, they will fall into a trap.
It is assumed that bots know the entire geometry of the world, i.e. location of all obstacles.



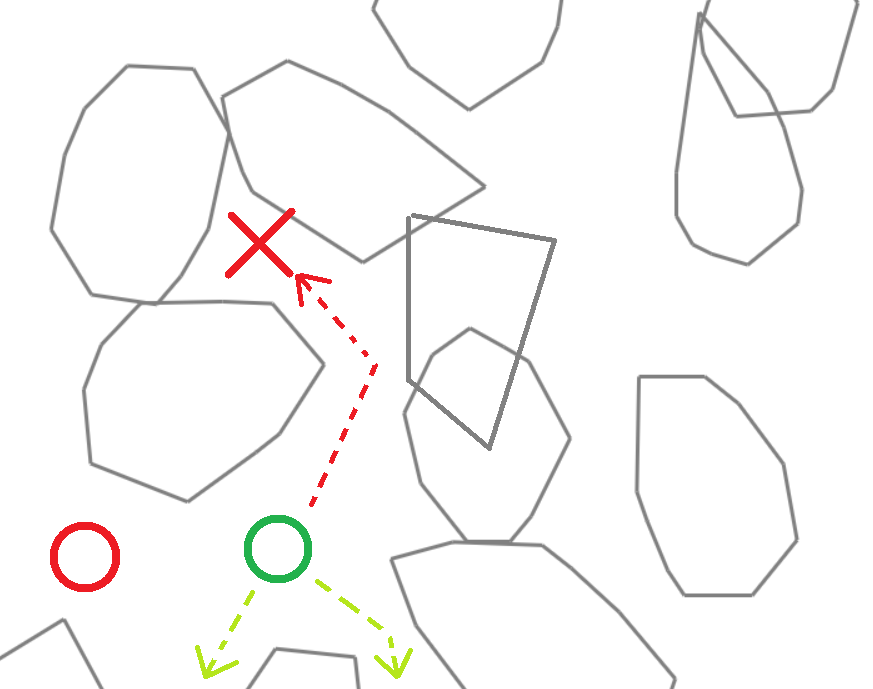
What algorithm should green bots have?

Answer 1

convert your plane to a graph. For example, through navmesh. Then you just need to move along those vertices of the graph that will allow you to return to the starting point / goal without going through the same route twice. Moreover, such blind spots-hangs can be weeded out altogether at the stage of building the world.

Answer 2

Let them mark the road, both of them, with their own color.

The navigation of the red bots uses a graph.

Weigh the edges of the graph. On these scales, it is already possible to do some kind of analysis. For example, from where only the Reds return, it is better for the Greens not to go there. The ant algorithm in general.

Answer 3

The problem lies in the setting itself. It is not enough for the bot to run away from the reds. He needs to lay out the trajectory in advance so that at equal speeds they both run endlessly. I understand that it will be a success.
All other algorithms at equal speeds gravitate to the fact that the green will be getting closer and closer. He needs to get into corners. And all known short-range machine algorithms require feeling or touching dead ends and corners. In this scenario, the green will be caught. Or it is necessary to give him a head start in speed.