How to implement the player pursuit algorithm taking into account polygon obstacles?

Question

JavaScript

There is a large rectangular map (5000 x 5000 px) and a list of bulging obstacle polygons (100-500 obstacles). And there are also bots (10-50 pieces), which should pursue the player without interfering with each other.

I had this idea:
Release 2 segments-sensors from each bot, initially both directed at the player. And while these rays cross the polygons, rotate (one clockwise, the other against) them (by a small angle) until they stop crossing the polygons. And then direct in the direction of the beam, which previously stopped crossing the polygons.

But this idea:
Firstly, it is very time-consuming. (it is necessary to check from each bot the rays that also rotate whether they intersect with each edge of the polygon, of which there are many).

Secondly, it does not always lead to the expected results:
If the beam length is too short, then the bot can get into a dead end, and then it will have to get out of it (and this is clearly not the optimal route) the

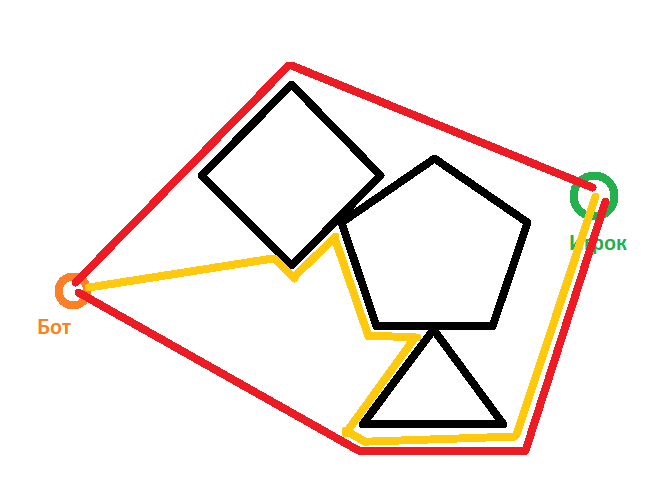
bot will go the orange path, when red is clearly more optimal.

However, if the beam length is too long, then the bot will take the narrow passage as a dead end, and will bypass it

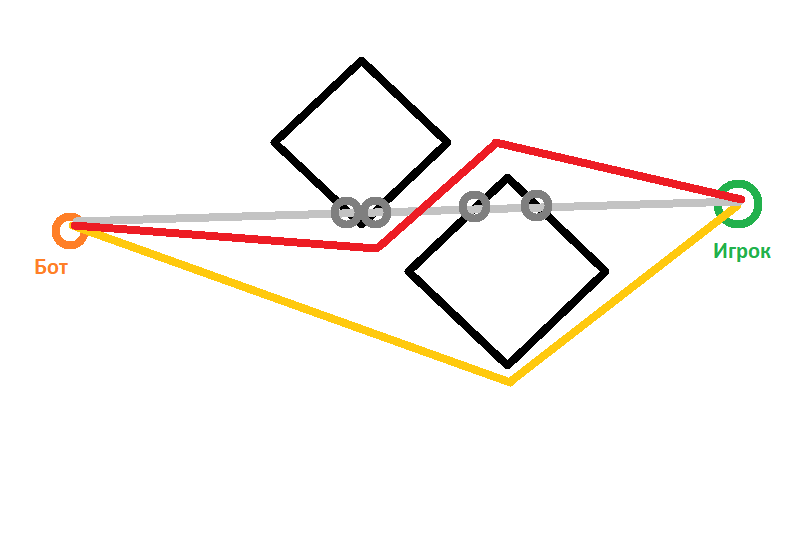
. Gray is the sensor that crossed the polygons, so the bot will go orange, although red is also better.

And here it is not clear whether there is a compromise on the length of the sensor, so that it bypasses dead ends and does not confuse them with narrow passages?

And thirdly, the bots interfere with each other, but this can probably be solved here, taking into account not only obstacles, but also other bots

I have found many solutions for cell maps, for example this one
. However, I don't have cells. And if I divide the entire field into cells, then the field will be too large, and this will affect performance (after all, the player does not stand still, but runs away).

I also found a solution through the navigation mesh (Nav Mesh), like this.
However, it says that firstly, it does not always produce the shortest path (The astar heuristic & cost functions need another pass. They don't always produce the shortest path. Implement incomplete funneling while building the astar path?).
And secondly, we need rectangular polygons here.(Allow non-square navmesh polygons from Tiled - ideally, any convex shape.). But I have not only rectangular polygons.

Well, the question arises how to implement the task: Generation of a path for the bot in real time to the player with optimal obstacle avoidance (polygons) and taking into account the trajectory of other bots

Answer 1

If the bots must bypass the polygons at some distance (they cannot touch them, as you have in the picture), then inflate all polygons by this radius (for each vertex, find 2 outward normals to neighboring sides, shift the sides by r along these normals and cross). You can derive a formula on a piece of paper through cosines / sines between normals (ie vector / scalar product of normals). It will be necessary to add both normals to the point, multiplied by 1/(cos(a/2)*sqrt(2+2cos(a))), where a is the angle between the normals.
Bots can now be considered points and can touch polygons.
Build a graph. The vertices in the graph are polygon vertices, bots and the player. For each vertex and another polygon, find 2 tangents from a point to a polygon - you can go through all the segments from a vertex to another polygon and discard those with respect to which 2 sides of the second polygon lie on opposite sides. Also check all these tangents for intersections with all other polygons and delete those that intersect (check each side of the polygon, and intersect the side with a known tangent segment).
Now you have only tangents that make sense to walk. Add them to the graph (the lengths of the edges are equal to the lengths of the segments).
Also add all polygon edges to the graph. All shortest paths to all points go in this graph. You either walk along the polygon, or go from the current point tangentially to some polygon. Obviously, any other path can be improved until it consists of these pieces.
Now, for each bot and player, do the same - build tangents to all polygons, remove those that intersect with other polygons. Also add direct player-bot paths if there are no intersections with polygons. In this graph, you need to find the shortest paths (better Dijkstroy from the player to all the bots).
Bypassing other bots is done like this - bots have calculated paths. The bots are trying to take small steps along the path. If they intersect with another bot, then you can skip the turn, or try to push the other bot. Give the bots random priorities and if the higher priority bot wants to cross paths with the lower priority bot, the second one takes a step back.
They will crowd into narrow passages, but eventually they will line up and follow each other. But this is if the player is alone. Then the bots go in one direction. If they can walk against each other, it will be worse. They can lock each other in a narrow passage and push each other out for a long time.
Now - recalculation when the player moves. Periodically it is necessary to recalculate the paths for bots. To do this, you need to rebuild the tangents from the player and bots to polygons and drive Dijkstra again.
Now about speed. You can do just as I described above. All you need is to be able to check that 2 line segments intersect and that the polygon lies on the same side of the ray. Well, Dijkstra's algorithm.
You build tangents between obstacles only once, here speed is not so important. Worse with dots bots and the player. Here tangents should be searched often. If the polygons are very large, then you can search for intersection points and tangents for the logarithm, but these are very abstruse algorithms, through a ternary search. I can write later if needed.
The slowest thing is to check for intersections with all polygons for each tangent (this is n ^ 2 checks if you have n polygons). Here you can also very cleverly speed up to n log n checks if all tangents are sorted by angle and then do something like a sweeping line algorithm, but rotate your gaze around a point. It is quite difficult to even describe, let alone implement. We need to stack the polygons into something like a balanced search tree that will keep them in sorted order relative to the distance to the point. Each tangent either adds a polygon or removes one. You only add a tangent if the polygon was the nearest one when you added or removed a polygon. Here you will need to be able to determine the distance from a point to a polygon along a straight line. Again, you can do a ternary search on the points of the polygon.
There is also an option through BSP (as in Duma. Indeed, this task is, in fact, to find out which polygons are visible from any point. Very close to computer graphics). It is necessary to divide the entire plane into regions and store for each region which polygons have tangents from it. To do this, all sides of the polygons must be extended to straight lines. Cross everything with everything, select areas. Then, for any point in each area, construct tangents and save. Then combine all these areas into BSP. This is a very good speedup, but it only works if you have a static map. You can precalculate and write to the file already BSP.
Finding a path in a graph can also be sped up. Without adding bots and a player to the graph, find all shortest paths using Floyd's method. Now that you have built all the tangents, for each bot iterate over its tangent and the tangent from the player. You can instantly calculate the shortest path through these tangents, because part of the path inside the graph on polygons is already pre-calculated from Floyd's algorithm. This will be noticeably faster than running the dijkstra each time, because the tangents are much smaller than the vertices of everything in the graph.

Answer 2

If there are obstacles with corners and there is no direct path, then at first glance it seems that the bot should move around the corners. So you can represent the corners of the obstacle as the vertices of the graph (the bot and the player are also vertices) and find the path from the vertex where the bot is located to the vertex of the player. Paths between vertices may have a cost (the length of the path), some paths may be blocked (for example, by other bots if they stay there for a long time)

Answer 3

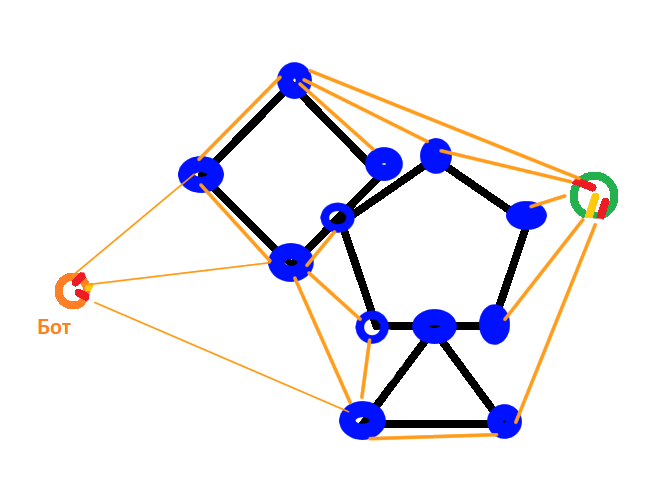
Divide the field into cells, this is best, and think about whether it is important for you to find exactly the shortest path or you can use A * with a heuristic algorithm .
Well, you need to think about optimization if the speed is not sufficient, the larger the size of the cell, the faster the algorithm will work, but the less accuracy, you should not make the size of the cells larger than the size of the bot (it just may not fit into small gaps). No need to look for a path at every step, do it less often. It may be worth looking for a path not for each bot separately, but for example, it takes a bot and everyone who is within a certain radius and line of sight from it and we are looking for a path for this entire group. Well, first do it in the most unoptimized way, and then look at the speed of work

Answer 4

The pathfinding algorithms are called A star . Yes, the examples are mostly done on cell fields, but, in the very definition of the algorithm:

a search algorithm that finds the least cost path from a start vertex to a chosen end vertex in a weighted graph.

Nothing is said about the fact that it works only on the cell field. So I would look for examples of the implementation of this algorithm - for sure there will be one that suits you.

Answer 5

Since the map is rectangular (or can be described by a grid) and its size is small (5K * 5K is small), then the ideal solution is wave tracing, which is also one of the breadth-first search implementations. There will be a shortest path, but each polygon must first be "drawn" into the grid so that the cell cannot be entered.