How to get back now? How to find out the equation of a parabola in the old basis?

Question

Mathematics

Hello! Tell me, please. There is a task: Find the equation of a parabola if it is known that it passes through the points (0,0) (0,1), and the line y \u003d x-1 serves as its axis of symmetry
The idea is this: rotate the basis by 45 and shift to the left by 1

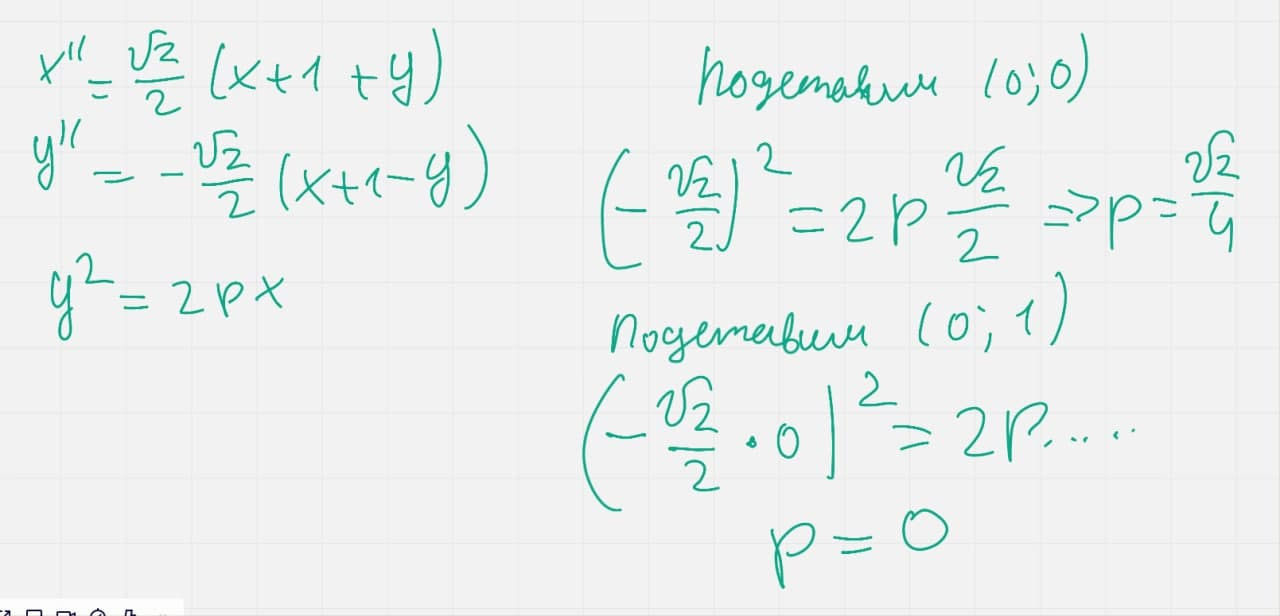
Here I expressed the new coordinates through the old ones and immediately substituted the points to find out the parabola equation in the new basis? How true and how to go back to the old basis? Something stupid

Answer 1

1. Shift the coordinate system down by 1.
x' = x
y' = y + 1
Inverse transformation:
x = x'
y = y' - 1
Straight line equation: y = x − 1, y' − 1 = x' − 1 , y' = x'
Transition of points: (0, 0) → (0, 1), (0, 1) → (0, 2)
2. Rotate the coordinate system clockwise by π/4.
x'' = x'⋅cos(π/4) − y'⋅sin(π/4) = x'⋅√2/2 − y'⋅√2/2
y'' = x'⋅sin(π/ 4) + y'⋅cos(π/4) = x'⋅√2/2 + y'⋅√2/2
Inverse transformation:
x' = x''⋅cos(π/4) + y''⋅sin (π/4) = x''⋅√2/2 + y''⋅√2/2
y' = −x''⋅sin(π/4) + y''⋅cos(π/4) = − x''⋅√2/2 + y''⋅√2/2
Equation of a straight line: y'
Point transition: (0, 1) → (−√2/2, √2/2), (0, 2) → (−√2, √2)
Equation of a parabola symmetrical to the y-axis: y'' = a⋅x '' ² + b
a/2 + b = √2/2
2⋅a + b = √2
Hence a = √2/3, b = √2/3
y'' = √2/3⋅x'' ² + √2/3
x'⋅√2/2 + y'⋅√2/2 = √2/3⋅(x'⋅√2/2 − y'⋅√2/2) ² + √2/3
x ' ² + y' ² ​​− 2⋅x'⋅y' − 3⋅x' − 3⋅y' + 2 = 0
x ² + (y + 1) ² − 2⋅x⋅(y + 1) − 3⋅ x − 3⋅(y + 1) + 2 = 0
x ² + y ² − 2⋅x⋅y − 5⋅x − y = 0