How to fit an arbitrary figure into a figure that consists of N x M rectangles?

Question

Mathematics

Hello!
In which direction to dig when solving this problem?
I'll explain it a little graphically:
A certain rectangular area of ​​size N x M is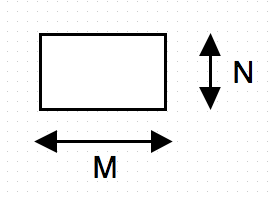

set. A certain arbitrary area is set, which must be inscribed in a figure that can be assembled from the rectangles described above. In a simple case, it might look like this: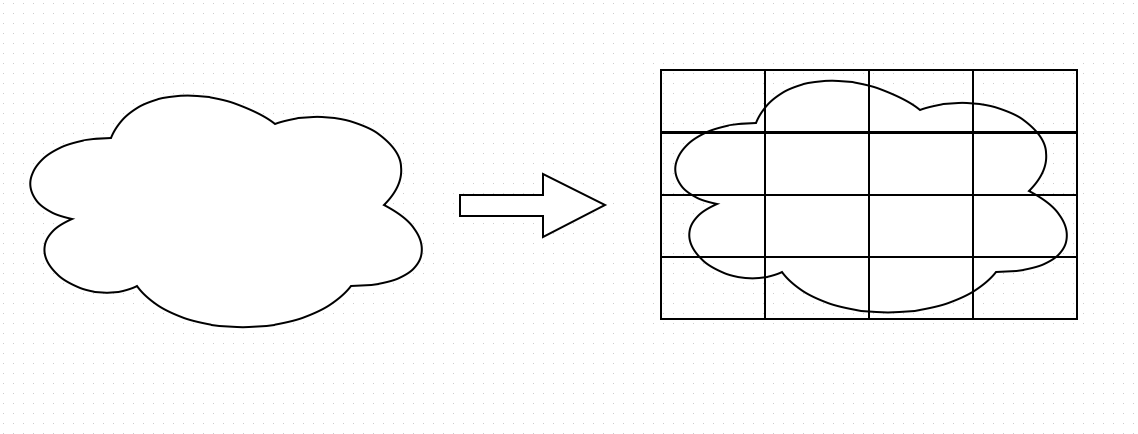

Rectangles don't have to be right next to each other. It is possible (and even better) for them to run into each other.
I will be glad to algorithms from the good old mathematics, useful articles, links to the forum or pseudocode.
update:
There is also an optimization problem to reduce the number of rectangles. For example, in the example picture, the left side of the figure is covered with four rectangles. If you remove the top left (or bottom left) and move the remaining three rectangles up (down), you can cover the area of ​​the shape with three rectangles.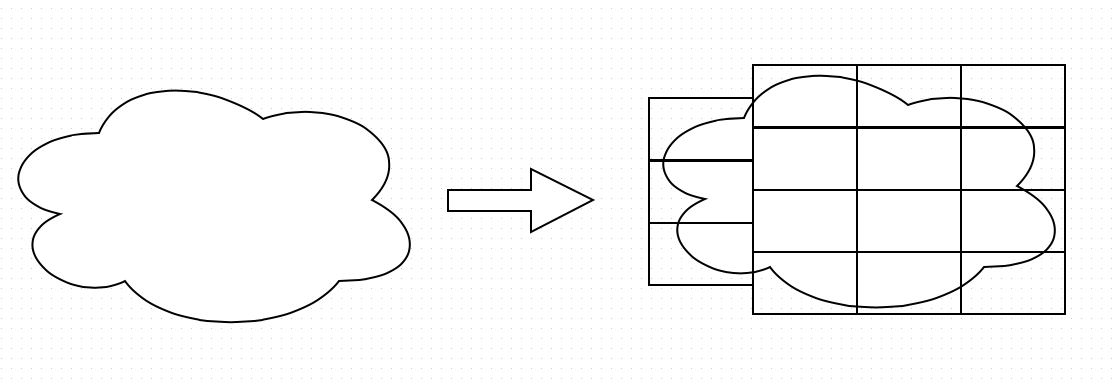

Update2:
The figure to fit is specified using a set of points on the plane. For example, an array [{x1,y1}, {x2,y2},{x3,y3}] comes in and connecting them one by one, a triangle will be obtained.
In the simplest case, the points will be connected by straight lines. Connection using splines is not yet considered.

Answer 1

Split the area into a grid of small rectangles like you have in the picture. Walk through each rectangle and find out if the shape passes through it. No - we delete the rectangle, yes - we leave it.
After that, you can merge all adjacent rectangles to reduce their total number.